30. Операция сложения векторов и ее свойства
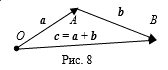
Определение 11. Суммой двух векторов A и B, называются такой третий вектор С, обозначаемый символом A + B, который изображается направленным отрезом ![]() , построенным следующим образом: из любой точки O откладывается направленный отрезок
, построенным следующим образом: из любой точки O откладывается направленный отрезок![]() = A, из точки А откладывается направленный отрезок
= A, из точки А откладывается направленный отрезок ![]() = B.
= B.
|
Теорема 5. Сумма A + B любых двух векторов A и B определяется однозначно.
Доказательство. В силу теоремы 4 достаточно доказать, что сумма векторов не зависит от выбора начальной точки О. Построим две суммы A + B векторов A и B, выбирая в качестве начальных точек две различные точки О И О¢ (см. рис 9). Покажем, что ![]() . Так как
. Так как ![]() И
И ![]() , то по следствию 2 теоремы 3
, то по следствию 2 теоремы 3 ![]() И
И ![]() . Тогда по теореме 2
. Тогда по теореме 2 ![]() . Отсюда, применяя следствие 2 теоремы 3 получаем
. Отсюда, применяя следствие 2 теоремы 3 получаем![]() .
.

Теорема 6. Для любых векторов A, B, C Справедливы свойства:
1) A + B = B + A - Коммутативный закон сложения;
2) A + (B + C) = (A + B) + C - Ассоциативный закон сложения;
3) A + 0 = A - Свойство нулевого вектора;
4) A + (-A) = 0 - Свойство противоположно
Доказательство. Справедливость свойств 1 и 2 вытекает из определения 11 (см. рис. 10 и 11), а свойств 3 и 4 из определений нулевого и противоположного векторов.

Сумму двух неколлинеарных векторов A и B можно найти по Правилу параллелограмма . Для этого необходимо из одной точки O отложить оба вектора A = ![]() И B =
И B = ![]() и построить параллелограмм OADB на векторах
и построить параллелограмм OADB на векторах ![]() И
И ![]() (см. рис. 10). Тогда суммой A + B векторов A и B изображается направленным отрезком
(см. рис. 10). Тогда суммой A + B векторов A и B изображается направленным отрезком ![]() диагонали параллелограмма.
диагонали параллелограмма.
Сумму любого конечного числа векторов можно найти по правилу многоугольника (см. рис. 12).
| < Предыдущая | Следующая > |
|---|