22. Простейшие свойства векторного пространства

Рассмотрим те свойства векторного пространства, которые вытекают из его определения.

Свойство 1. В векторном пространстве V существует единственный нулевой вектор 0.

Доказательство. Допустим противное, что в V имеется два нулевых вектора 0 И Тогда по аксиомам 3° и 1° имеем

0 = 0 + = + 0 = .

Свойство 2. В векторном пространстве для любого вектора существует единственный противоположный вектор -.

Доказательство. Допустим противное, что для вектора имеется два противоположных вектора -A1 и -A2. Тогда по аксиомам 1° - 4° имеем

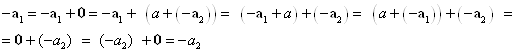
Определение 3. Разностью Двух векторов A и B, называются такой третий вектор С, обозначаемый символом A - B, при сложении которого с вектором B получаем вектор A.

Свойство 3. Для любых векторов A, B Разность A - B существует, единственна и вычисляется по формуле:

A - B = A + (-B).

Доказательство. См. доказательство теоремы 7 из §1.

Свойство 4. Для любых векторов имеем -(A + B) =(-А) + (-B).

Доказательство. По аксиомам 1° - 4° имеем

(A + B) +((-А) + (-B)) = (A + (-А)) +(B + (-B)) = 0 + 0 = 0.

В силу единственности противоположного вектора получаем -(A + + B) =(-А) + (-B).

Свойство 5. Для любого вектора Имеем -(-A) = А.

Доказательство. По аксиомам 1°, 3° A +(-А) = (-А)+A = 0 и в силу единственности противоположного вектора получаем -(-A)= А.

Свойство 6. Для любых векторов , если A + B = А + С, то B = С.

Доказательство. Прибавим к обеим частям равенства A + B = =А+ С вектор -А, по аксиомам 1° - 3° получим B = С.

Свойство 7. Для любых векторов Если A + B = А, то B = 0.

Доказательство. Следует из свойства 6.

Свойство 8. Для любого вектора Имеем 0×A = 0.

Доказательство. По аксиомам 8° и 6° имеем

A + 0×A = 1×A + 0×A = (1+0)×A = 0×A .

Отсюда по свойству 7 0×A = 0.

Свойство 9. Для любого числа Имеем a×0 = 0.

Доказательство. По аксиоме 5° имеем

A×A + a×0 = a×(А + 0) = a×A .

Отсюда по свойству 7 a×0 = 0.

Свойство 10. Пусть , . a×А = 0 Тогда и только тогда, когда a=0 Или А = 0.

Доказательство. Достаточность условия следует из свойств 9 и 10, а необходимость докажем методом от противного. Допустим, что aА = 0 И или Так как Р - поле, то для существует обратный элемент . Тогда умножая обе части равенства aА = 0 На a-1 и пользуясь аксиомами 7 и 8 последовательно получаем