21. Примеры векторных пространств

Пример 1. Пространство скаляров. По определению поля следует, что любое поле Р является векторным пространством над самим собой относительно операций сложения и умножения в поле.

Пример 2. Рассмотрим множество V2 всех радиус векторов координатной плоскости с началом в начале координат, которые складываются по правилу параллелограмма и умножаются на числа поля R Как геометрические векторы. Из свойств геометрических векторов следует, что V2 является векторным пространством над полем R.

Пример 3. Пространство матриц. Пусть - множество всех матриц размерности M ´ N с элементами из поля Р. По определению и свойствам операций сложения матриц и умножению матрицы на число, это множество является векторным пространством над полем Р, его называют Векторным пространством m´N - матриц над полем Р.

Пример 4. Арифметическое или координатное N-мерное пространство. N - мерным числовым вектором над полем Р называют упорядоченный набор из N чисел поля Р. Числа называются Координатами числового вектора. Множество всех N - мерных числовых векторов обозначается символом Рn.

Пусть A=(a1, a2,...,an), B=(b1, b2,...,bn) два N - мерные числовые вектора.

Два N - мерных числовых вектора называются Равными, если все соответствующие координаты векторов попарно равны.

Суммой N - мерных числовых векторов называется такой n - мерный числовой вектор, каждая координата которого равна сумме соответствующих координат данных векторов, т. о.

A=(a1+b1,a2+b2,...,an + bn).

Произведением N - мерного числового вектора на число называется такой n - мерный числовой вектор, каждая координата которого равна произведению числа K на соответствующую координату данного вектора, т. о.

KA = (KA1, KA2,...,KAn).

Заметим, что N - мерные числовые вектора являются матрицами размерности 1´N и операции сложение и умножение на число совпадают с матричными операциями. Поэтому множество Рn является векторным пространством над полем Р. Оно называется N-мерным арифметическим или Координатным пространством, Или Пространством строк Длины N над полем Р.

Аналогично рассматривается Пространство столбцов из N элементов над полем Р.

Пример 5. Пространство функций. Пусть Х - произвольное множество, F(X) - множество всех функций на X со значениями в поле Р , т. е. отображений X в Р. Если такое отображение, то F(X) обозначает значение F на элементе

Сумма F+G функций F и G и произведение a F функции F на число определяются поточечно:

(F+G)(X)=F(X)+G(X), для любых

(aF)(X)=a(F(X)), для любых .

Множество F(X) является векторным пространством над полем Р . Оно называется Пространством функций на Х со значениями в поле Р.

Действительно, ранее было доказано, что множество F(X) является аддитивной абелевой группой (см. пример 1.4.1), т. е. выполняются условия 1), 1°-4° определения 1.

Доказывая условие 2) заметим, что произведение числа на функцию есть функция, определенная на Х со значениями в Р, т. е и она определена однозначно.

Условия 5°-8° проверяются на основании определения равенства функций. Проверим, например, условие 5°, которое в нашем случае принимает вид:

Так как области определений функций, стоящих в правой и левой частях этого равенства, равны и для любого X€X

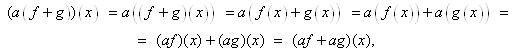
То указанное выше равенство выполняется.

Из приведенных выше примеров следует, что векторные пространства встречаются во всех разделах математики и заслуживают пристального изучения.

< Предыдущая		Следующая >