18. Элементарные матрицы
Определение 8. Элементарными матрицам называются такие матрицы, которые получаются с помощью одного элементарного преобразования из единичной матрицы.
Таким образом элементарные матрицы получаются из единичной матрицы с помощью следующих элементарных преобразований: 1) перестановка двух строк (I-й и j-й) местами; 2) умножение какой-нибудь строки (I-й) на число С≠0; 3) прибавление к какой-нибудь строке (I-й) другой строки (J-й), умноженной на число С. Они имеют соответственно следующий вид (первой указана единичная матрица, из которой получены следующие за ней элементарные матрицы, в каждой матрице выделены I-я и j-я строки и I-й и j-й столбцы):
 ,
,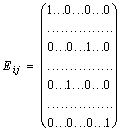 ,
, ,
, .
.
Элементарные матрицы обладют следующими свойствами.
1. Определители элементарных матриц не равны нулю и
![]() .
.
2. Элементарные матрицы обратимы и обратные матрицы для элементарных матриц являются элементарными матрицами:
![]() .
.
3. Если матрицу А порядка n умножить слева на элементарную матрицу порядка n, то с матрицей А произойдет элементарное преобразование с помощью которого элементарная матрица получена из единичной матрицы.
Свойство 1 следует из свойств определителя, свойство 2 доказывается с помощью непосредственного вычисления обратных матриц по алгоритму из теоремы 5, свойство 3 проверяется с помощью умножения матрицы А Слева на элементарные матрицы.
Теорема 8. Для любой невырожденной матрицы А существует такая последовательность элементарных матриц Е1, Е2,..., Еk , Что
![]() . (12)
. (12)
Доказательство. По теореме 2 парарафа 1 существует такая последовательность элементарных преобразований ![]() строк, которые переводят матрицу А порядка N в матрицу С ступенчатого вида. Так как элементарные преобразования не обращают определитель матрицы в нуль, то никогда не получится матрица с нулевой строкой, и строки матрицы не будут выбрасываться. Поэтому матрица С квадратная матрица ступенчатого вида порядка N. Элементарным преобразованиям
строк, которые переводят матрицу А порядка N в матрицу С ступенчатого вида. Так как элементарные преобразования не обращают определитель матрицы в нуль, то никогда не получится матрица с нулевой строкой, и строки матрицы не будут выбрасываться. Поэтому матрица С квадратная матрица ступенчатого вида порядка N. Элементарным преобразованиям ![]() соответствуют элементарные матрицы Е1, Е2,..., Еu . Пусть J1 переводит матрицу А в А1, J2 переводит А1 в А2 , и т. д. JU переводит Аu-1 в Аu=B. Тогда
соответствуют элементарные матрицы Е1, Е2,..., Еu . Пусть J1 переводит матрицу А в А1, J2 переводит А1 в А2 , и т. д. JU переводит Аu-1 в Аu=B. Тогда
![]() ,(13),
,(13),
Где В ступенчатая (треугольная) матрица вида:
![]()
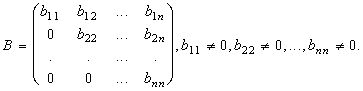
Умножим строки этой матрицы соответственно на числа ![]()
И матрица В преобразуется к виду: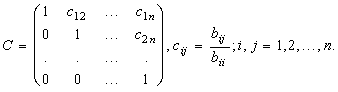
Приведем матрицу С к единичной матрице. Для этого умножим прибавим к 1-й, к 2-й, и т. д. к (N-1)-й строкам матрицы N-ю строку, умноженную соответственно на числа ![]() получим все нули в последнем столбце матрицы С кроме элемента N-й стоки (все остальные элементы матрицы С не меняются). Аналогично продолжая элементарные преобразования получим из матрицы С единичную матрицу.
получим все нули в последнем столбце матрицы С кроме элемента N-й стоки (все остальные элементы матрицы С не меняются). Аналогично продолжая элементарные преобразования получим из матрицы С единичную матрицу.
Следовательно, существует такая последовательность элементарных преобразований ![]() строк, которые переводят матрицу В порядка N к единичной матрице Е. Элементарным преобразованиям
строк, которые переводят матрицу В порядка N к единичной матрице Е. Элементарным преобразованиям![]() соответствуют элементарные матрицы Еu+1 , ЕU+2,..., Еk . Пусть JU+1 переводит матрицу B в B1, JU+2 переводит B1 в B2 , и т. д. JK переводит Bk-u в E. Тогда
соответствуют элементарные матрицы Еu+1 , ЕU+2,..., Еk . Пусть JU+1 переводит матрицу B в B1, JU+2 переводит B1 в B2 , и т. д. JK переводит Bk-u в E. Тогда
![]() .
.
Подставляя в это равенство формулу (13) находим, что
![]() .
.
Теорема доказана.
Умножая обе части равенства (12) последовательно на ![]() находим, что
находим, что ![]() и получаем следующее следствие.
и получаем следующее следствие.
Следствие 1. Любую невырожденную квадратную матрицу А порядка n можно представить в виде произведения элементарных матриц порядка n.
Из равенства (12) в силу теоремы 6 находим, что
![]() .
.
Отсюда видно, что если мы к матрице Е применим ту же самую цепочку элементарных преобразований строк, с помощью которой из матрицы А мы получили единичную матрицу, то из матрицы Е мы получим обратную матрицу А-1. Отметим, что эти преобразования можно выполнять одновременно, а для этого достаточно справа к матрице А приписать единичную матрицу того же порядка.
Исходя из этого мы приходим к следующему способу вычисления обратной матрицы методом элементарных преобразований. Приписываем к матрице А срава единичную матрицу Е того же порядка, разделив их вертикальной чертой. Затем матрицу А с помощью элементарных преобразований строк приводится к единичной матрице Е (если в преобразованной матрице появится нулевая строка, то detA=0 и обратная матрица А-1 не существует). Тогда на месте приписанной матрицы Е получается матрица А-1.
Пример 4. Вычислить обратную матрицу для матрицы
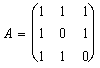 .
.
Припишем справа к матрице А единичную матрицу и приведем матрицу А элементарными преобразованиями к единичной матрице.
 .
.
Таким образом
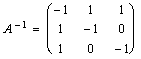 .
.
| < Предыдущая | Следующая > |
|---|