17. Матричные уравнения и системы линейных уравнений

Пусть А квадратная матрица порядка N, матрица В имеет n строк, матрица С имеет N столбцов. Рассмотрим следующие матричные уравнения:

, (5)

И

, (6)

Где X и Y неизвестные матрицы.

Теорема 6. Если detA≠0 , То каждое из уравнений (5) И (6) разрешимо, имеет единственное решение, решения находятся соответствеено по формулам:

(7)

И

. (8)

Доказательство. Рассмотрим уравнение (5), так как уравнение (6) рассматривается аналогично. Покажем сначала, что если Х0 решение уравнения (5) то оно находится по формуле (7). Действительно, имеем равенство А×Х0=В. Умножаем обе части этого равенства на А-1 и последовательно находим

Покажем теперь, что матрица, найденная по формуле (7) является решением уравнения (5):

Докажем, что решение уравнения (5) единственно. Действительно, если Х1 и Х2 решения уравнения (5) то выполняются равенства:

А×Х1=В и А×Х2 =В.

Приравнивая левые части этих равенств последовательно получаем

Теорема доказана.

Запишем систему линейных уравнений, воспользовавшись определениеми равенства и умножения матриц.

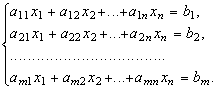(9)

Система (9) равносильна матричному равенству

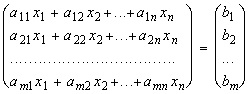
Или

,

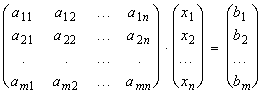АХ=В, (10)

Где А - матрица систем, В - столбец свободных членов, Х - столбец неизвестных. Отметим, что система (9) равносильна матричному уравнению (10). Тогда по теоремы 6 получим следующее предложение.

Теорема 7. Пусть в системе линейных уравнений (9) Число уравнений равно числу неизвестных (m=n) и d=detA≠0. Тогда система линейных уравнений (9) Имеет единственное рашение, которое находится по формуле

Х=А-1×В. (11)

По формуле (11) и способу вычисления обратной матрицы получаем

,

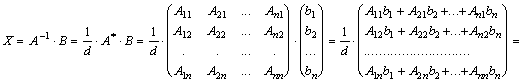
Где Di получается из D заменой I-го столбца столбцом свободных членов. Отсюда получаем найденные ранее формулы Крамера:

.

< Предыдущая		Следующая >