16. Обратная матрица

Определение 6. Единичной матрицей порядка n называется такая матрица порядка n, у которой на главной диагонали стоят единицы, а остальные элементы нули. Обозначаем буквой Е :

DIj - символ Кронекера,

Л. Кронекер (1823-1891) - немецкий математик, занимался в основном алгеброй и теорией чисе.

Отметим, что detE=1.

Определение 7. Пусть А квадратная матрица порядка N. Матрица A-1 называется обратной матрицей для матрицы А, если

. (3)

Теорема 5. Обратная матрица для матрицы А существует тогда и только тогда, когда detA≠0, При этом обратная матрица находится единственным образом.

Если определитель матрицы А не равен нулю, то матрица А называется Невырожденной или Неособенной матрице. В силу теоремы 5 A-1 существует тогда и только тогда, когда матриц А невырожденная.

Доказательство. 1. Необходимость. Пусть для матрицы А существует обратная матрица A-1. Тогда по определению А× A-1=Е. Переходя к определителям и пользуясь теоремой 5 получим: . Отсюда detA=|А|≠0. Необходимость доказана.

2. Достаточность. Пусть дана

, |А|=D≠0.

Построим матрицу A-1 следующим образом. Заменим каждый элемент матрицы А его алгебрамческим дополнением и получим матрицу

Полученную матрицу транспонируем и находим матрицу

(эта матрицы называется присоединененной или взаимной матрице к матрице А). Докажем тогда, что

. (4)

Для этого докажем равенства (3).

По следствию из теоремы о разложении определителя по элементам ряда

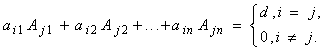
Тогда

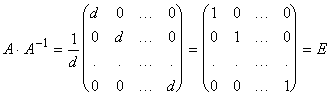Аналогично доказывается, что A-1×A=E.

Доказывая единственность обратной матрицы, допустим противное, что матрица А имеет две обратные матрицы . Тогда по определению и свойствам умножения матриц имеем

Теорема доказана.

Доказательство этой теоремы дает алгоритм для вычисления обратной матрицы.

Пример 3. Найти обратную матрицу для матрицы

Вычислим определитель матрицы A,

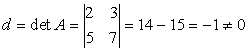Тогда обратная матрица существует. Вычислим алгебраические дополнения матрицы А и составим матрицу из алгебраических дополнений.

Транспонируем полученную матрицу:

Отсюда

< Предыдущая		Следующая >