15. Теорема об определителе произведения матриц
Теорема 4. Определитель произведения двух квадратных матриц А и В порядка n равен произведению определителей этих матриц, т. е.
![]()
Или
![]() .
.
Доказательство. Пусть
 ,
,  .
.
Тогда
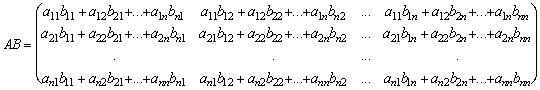 ,
,
Так как каждый элемент 1-й строки матрицы АВ есть сумма N чисел, то свойству определителя сам определитель есть сумма N, у которых каждый элемент каждой строки, начиная со второй (в том числе и 2-й) сумма N чисел. Тогда каждый из полученных N определителей разлагается на N определителей, а определитель матрицы АВ разлагается на сумму N2 определителей, у которых каждый элемент каждой строки, начиная с третьей (в том числе и 3-й) сумма N чисел. Продолжая этот процесс, представим определитель матрицы АВ в виде суммы Nn Определителей:
 .
.
Общие множители каждой из строк выносим за знак определителя и поучаем:
 .
.
Если среди чисел ![]() есть равные, то в соответствующем определителе указанной выше суммы будет имется по кравйней мере две равные строки и определитель обратится в ноль. Поэтому в этой сумме останутся только такие слагаемые, которые соответствуют попарно различным числам
есть равные, то в соответствующем определителе указанной выше суммы будет имется по кравйней мере две равные строки и определитель обратится в ноль. Поэтому в этой сумме останутся только такие слагаемые, которые соответствуют попарно различным числам ![]() . Тогда эти числа образуют N-перестановку из чисел 1,2,...,N. В сумме останутся только такие слагаемые, которым соответствуют престановки
. Тогда эти числа образуют N-перестановку из чисел 1,2,...,N. В сумме останутся только такие слагаемые, которым соответствуют престановки
![]() , (2)
, (2)
И сумма запишется в виде:
 .
.
В определителе, который стоит под знаком суммы, переставим строки так: если ![]() , то оставим первую строку на своем месте, в противном случае переставим первую строку и ту, в которой
, то оставим первую строку на своем месте, в противном случае переставим первую строку и ту, в которой ![]() ; если
; если ![]() , то оставим первую строку на своем месте, в противном случае переставим первую строку и ту, в которой
, то оставим первую строку на своем месте, в противном случае переставим первую строку и ту, в которой ![]() ; и т. д. после T престановок строк определитель под знаком суммы будет равен:
; и т. д. после T престановок строк определитель под знаком суммы будет равен:
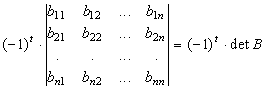 .
.
Если в соответствии с указанными выше перестановками строк в определителе мы будем производить перестановки (транспозиции) столбцов в подстановке (2), то после T транспозиций подстановка (2) перейдет в единичную подстановку. Так как единичная подстановка имеет знак +1 и каждая транспозиция меняет знак на противоположный, то знак подстановки (2) ![]() . Поэтому
. Поэтому

 .
.
Теорема доказана.
| < Предыдущая | Следующая > |
|---|