14. Транспонирование матриц

Операция транспонирования матриц, определенная в 1.2, определение 9, обладает следующими свойствами.

Теорема 4. Для любых матриц А, В соответствующей размерности и любого чисела A€K Справедливы следующие свойства.

1. .

2.

3.

4..

Доказательство. Доказательства этих свойств основываются на определении 2.2.9, определениях 1-5 и свойствах операций в кольце К. Докажем, например, свойство 4.

Пусть матрицы соответственно размерностей M´N, N´K (обозначены только общие элементы этих матриц). Тогда Существуют и матрица размерности M´K:

.

По определению преобразования транспонирования:

,,

.

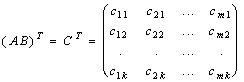Так как Матрицы размерностей K´N, n´M, то произведение существует и

.

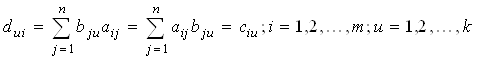Свойство доказано.

< Предыдущая		Следующая >