13. Умножение матриц

Отметим, что перемножать матрицы А и В можно только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Однострочная матрица называется Строкой, а одно столбцовая матрица называется Столбцом. Пусть даны строка А и столбец В одинаковой длины,

Определение 4. Произведением АВ строки А на столбец В той же длины называется сумма попарных произведений элементов строки на соответствующие элементы столбца, т. е.

Пусть число столбцов матрицы А равно числу столбцов матрицы В,

, .

Определение 5. Произведением АВ Матрицы А размерности m´N На матрицу В размерности n´K называется такая матрица С размерности m´K, каждый элемент которой сумма попарных произведений элементов I-й строки на соответствующие элементы j-го столбца, т. е.

. (1)

Таким образом для того, чтобы перемножить матрицы А и В необходимо умножить каждую строку матрицы А на каждый столбец матрицы В. Условие умножения двух матриц схематически можно изобразить следующим образом:

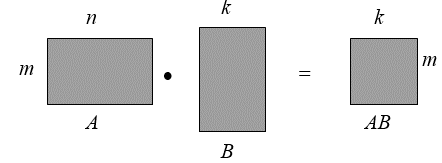
Пример 1.

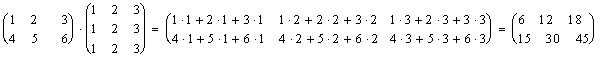Пример 2.

Последний пример показывает, что операция умножения некоммутативна даже для квадратных матриц.

Теорема 2. Для любых матриц А, В и С соответствующей размерности и для любых чисел A,B€K Справедливы следующие свойства.

1. (АВ)С=А(ВС) - Ассоциативность сложения.

2. (А+В)С=АС+ВС - правый дистрибутивный закон умножения относительно сложения.

3. А(В+С)=АВ+АВ - Левый дистрибутивный закон умножения относительно сложения.

4. A(АВ)=(AА)В=А(AВ) - ассоциативность умножения на число.

Доказательство. Доказательства этих свойств основываются на определениях 1-3, 5 и свойствах операций в кольце К. Докажем, например, свойство 1.

Пусть матрицы соответственно размерностей M´N, N´K, K´S (обозначены только общие элементы этих матриц). Тогда Существуют и матрицы соответственно размерностей M´K, n´S:

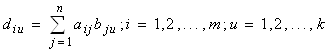Отсюда матрицы имеют одинаковые размерности M´S. Докажем, что соответствующие элементы этих матриц равны. Действительно, в силу приведенных выше формул

Для . Свойство доказано.

Обозначим множество всех квадратных матриц порядка n c элементами из кольца К черех . называется Матричным кольцом.

< Предыдущая		Следующая >