119. Конические поверхности

Определение 1. Пусть в пространстве дана линия L и точка S. Конической поверхностью S с направляющей L и вершиной S называется множество всех точек прямых проходящих через точку S и пересекающих кривую L. Линия L называется Направляющей конической поверхности S, прямые, из которых состоит коническая поверхность, называются Образующими Конической поверхности S.

Пусть направляющая L конической поверхности S Лежит в плоскости, параллельной координатной плоскости OXy, И задана уравнением

F(X,Y) = 0, Z = H; (1)

S(X0,Y0, Z0) - вершина конической поверхности, система координат аффинная.

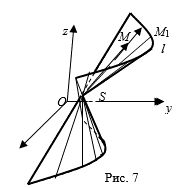
Уравнение конической поверхности

X

. (6)

Уравнение конической поверхности, направляющая которой задается уравнениями:

F(X,Y) = 0 , Z = H,

А вершина которой находится в начале координат S(0,0,0). Тогда по формуле (6) находим уравнение конической:

. (7)

Пример 1. Уравнение конуса, направляющая которого является эллипсом:

, Z = с,

Имеет вид

. (8)

< Предыдущая		Следующая >