12. Матрицы. Сложение матриц и умножение матрицы на число
Литература
1. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 17-19.
2. Ермаков В. И. Общий курс высшей математики. М.: Инфра - М, 2000. с. 56-68.
3. Кремер Н. Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 9-16,26-35.
4. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 142-148, 183-190.
1. Определение матрицы было дано в первом параграфе этой главы. Рассматриваем матрицы с элементами из некоторого коммутативного кольца K . Пусть даны две матрицы A и B Равной размерности:
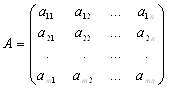 ,
,  .
.
Определение 1. Две матрицы A и B одинаковой размерности называются Равными, если соответствующие элементы матриц равны. Обозначаем ![]() .
.
Определение 2. Суммой двух матриц A и B одинаковой размерности называется такая матрица, обозначаемая A+B той же размерности, каждый элемент которой есть сумма соответствующих элементов матриц A и B :
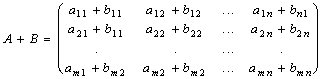 .
.
Определение 3. Произведением матрицы A на число A называется матрица, обозначаемая AA той же размерности, каждый элемент которой есть произведение числа A на соответствующий элемент матрицы A:
 .
.
Нулевой Матрицей называется такая матрица 0, все элементы которой равны нулю. Противоположной матрицей для матрицы A Называется такая матрицы - A , все элементы которой противоположны соответствующим элементам матрицы A. Таким образом
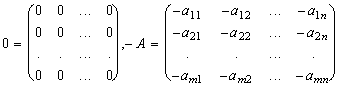 .
.
Теорема 1. Для любых матриц А, В и С И для любых чисел A,B€K Справедливы следующие свойства.
1. (А+В)+С=А+(В+С) - Ассоциативность сложения.
2. А+В=В+А - Коммутативность сложения.
3. Для любой матрицы А имеем А+0=А.
4. Для любой матрицы А имеем А+(-А)=0.
5. (A+B)А=AА+BА - Дистрибутивность относительно сложения чисел.
6. A(А+В)=AА+AВ - дистрибутивность относительно сложения матриц.
7. A(BА)=(AB)А - Ассоциативность умножения на число.
8. 1×А=А.
Доказательство. Доказательства этих свойств основываются на определениях 1-3 и свойствах операций в кольце К. Докажем, например, свойство 6.
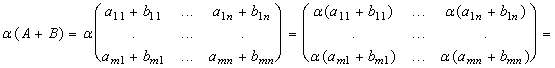
 .
.
| < Предыдущая | Следующая > |
|---|