118. Цилиндрические поверхности
Определение 1. Пусть в пространстве дана линия L и вектор S. Цилиндрической поверхностью S с направляющей L и образующими параллельными S называется множество всех точек прямых параллельных вектору S и пересекающих кривую L. Линия L называется Направляющей цилиндрической поверхности S, прямые, из которых состоит цилиндрическая поверхность, называются Образующими цилиндрической поверхности S.
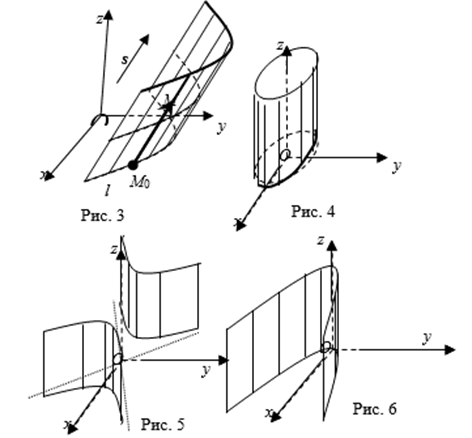
Пусть направляющая L цилиндрической поверхности S Лежит в плоскости, параллельной координатной плоскости OXy, И задана уравнением
F(X, y) = 0, Z = h; (2)
Направляющий вектор S = (M,K,N) не параллелен плоскости Oxy, система координат аффинная.. Уравнение цилиндрической поверхности:
![]() . (3)
. (3)
Пример 1. ПОверхность, определяемая уравнением
 ,
,
Является цилиндрической и называется Эллиптическим цилиндром (см. рис. 4).
Поверхность, определяемая уравнением
![]() ,
,
Является цилиндрической и называется Гиперболическим цилиндром (см. рис. 5).
Поверхность, определяемая уравнением
![]() ,
,
Является цилиндрической и называется Параболическим цилиндром (см. рис. 6).
| < Предыдущая | Следующая > |
|---|