117. Поверхности вращения

Определение 1. Пусть в пространстве дана прямая A и линия L, которая не лежит в плоскости, перпендикулярной прямой A. Поверхность S, которая получается вращением линии L относительно прямой A, называется Поверхностью вращения. Линия L называется Образующей поверхности вращения, Прямые называется Осью вращения.

Поверхность вращения состоит из окружностей, которые получаются вращением точек линии L относительно прямой A, и которые лежат в плоскостях перпендикулярных прямой A, с центрами на прямой A.

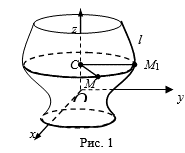
Усть образующая L поверхности вращения S Лежит координатной плоскости OYz, И задана уравнением

F(Y,Z) = 0, X = 0; (1)

Равнение поверхности вращения линии L Относительно оси Oz:

. (3.2)

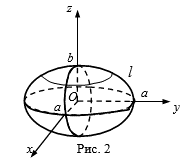
Пример 1. Поверхности вращения эллипса относительно оси Oz:

. (3.3)

Полученная поверхность называется Эллипсоидом вращения и изображена на рис. 2.

< Предыдущая		Следующая >