06. Подстановки и чётность подстановки
Определение 5. Подстановкой N-й степени называется взаимно однозначное отображение ![]() Множества
Множества ![]() самого на себя. Обычно подстановку записывают с помощью двух N-перестановок, записанных одна под другой:
самого на себя. Обычно подстановку записывают с помощью двух N-перестановок, записанных одна под другой:
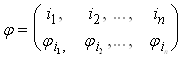 , (1)
, (1)
Где через ![]() обозначается число, в которое при подстановке
обозначается число, в которое при подстановке ![]() переходит элемент i, т. е.
переходит элемент i, т. е. ![]() ; i=1,2,...,N.
; i=1,2,...,N.
В записи подстановки можно произвольным образом менять столбцы местами. Например, все три указанные ниже подстановки равны.
![]()
![]() . (2)
. (2)
В частности всякая ![]() подстановка N-й степени может быть записана в виде:
подстановка N-й степени может быть записана в виде:
 .
.
При такой форме записи различные подстановки различаются только перестановками, стоящими в нижней строке. Тогда в силу теоремы 1 получили следующее утверждение.
Теорема 4. Число различных подстановок n-й степени равно N.
Определение 6. Числом инверсий в подстановке называется сумма числа инверсий в первой и второй строках подстановки.
Обозначаем число инверсий в подстановке ![]() символом
символом ![]() . Подстановка
. Подстановка ![]() называется Четной, если число
называется Четной, если число ![]() четное, и называется Нечетной если число
четное, и называется Нечетной если число ![]() нечетное. Знаком подстановки называется число:
нечетное. Знаком подстановки называется число:
![]() .
.
Таким образом знак подстановки ![]() равен 1 или -1 в зависимости от того четная подстановка
равен 1 или -1 в зависимости от того четная подстановка ![]() или нечетная.
или нечетная.
В силу теоремы 2 при перестановке столбцов в подстановке одновременно четности перестановок, стоящих в нижней и верхней строках подстановки, меняются на противоположные. Следовательно, четность перестановки сохраняется. Отсюда и из теоремы 3 получаем, следующие свойства подстановок.
1. Четность и знак подстановки не зависят от формы записи подстановки.
2. При N>1 число четных подстановок N-й степени равно числу нечетных подстановок и равно ![]() .
.
Пример 4. Подстановка (2) нечетная и имеет знак -1, хотя при различных формах записи имеет 3, 7, 5 инверсий.
Покажем, что множество всех подстановок N-й степени образует группу относительно операции умножения подстановок, определенной ниже. Эта группа имеет большое значение в алгебре, называется Симметрической Группой и обозначается символом ![]() .
.
Определение 7. Произведением подстановок ![]() и
и ![]() N-й степени называется композиция
N-й степени называется композиция ![]() Этих постановок как отображений, т. е. для любого
Этих постановок как отображений, т. е. для любого ![]() имеем
имеем ![]() . Обозначаем
. Обозначаем
Так как композиция двух биективных отображений биективное отображение, то произведение двух подстановок N-й степени есть подставок N-й степени. При практическом умножении подстановок сначала выполняется правая подстановка, а затем левая. Например,
![]() ,
, ![]() .
.
Теорема 5. Множество ![]() всех подстановок n-й степени образует группу относительно операции умножения подстановок.
всех подстановок n-й степени образует группу относительно операции умножения подстановок.
Доказательство. В силу сказанного выше операция умножения подстановок бинарная алгебраическая операция. Проверим аксиомы группы.
Умножение подстановок ассоциативно. Действительно, пусть ![]() . Тогда для любого
. Тогда для любого ![]()
![]()
И по определению равенства отображений ![]() .
.
Единичным элементом является Тождественная Подстановка
![]() .
.
Обратной подстановкой для подстановки ![]() Является подстановка
Является подстановка
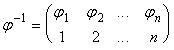 .
.
Действительно,
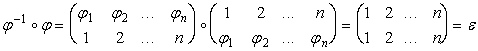 .
.
Аналогично показывается, что ![]() .
.
Следовательно, по определению множество ![]() группа. Теорема доказана.
группа. Теорема доказана.
Пример выше показывает, что группа ![]() некоммутативная, т. е. неабелева.
некоммутативная, т. е. неабелева.
| < Предыдущая | Следующая > |
|---|