07. Определение определителя
Понятие определителя возникло в связи с задачей решения систем линейных уравнений. Рассмотрим систему двух линейных уравнений с двумя неизвестными:
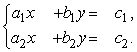 (3)
(3)
Решим эту систему методом исключения неизвестных. Для этого умножим первое уравнение на ![]() , а второе на
, а второе на ![]() ,
,![]() Сложим уравнения и получим:
Сложим уравнения и получим:
![]() . (4)
. (4)
Аналогично, исключая X , получим
![]() . (5)
. (5)
Выражение ![]() называется Определителем квадратной матрицы второго порядка и обозначается специальным символом
называется Определителем квадратной матрицы второго порядка и обозначается специальным символом
 .
.
Тогда, если через ![]() и
и ![]() обозначим определители:
обозначим определители:
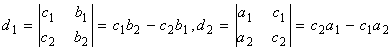 ,
,
То равенства (4) и (5) перепишутся в виде:
![]() .
.
Если ![]() , то из них находим
, то из них находим
![]() . (6)
. (6)
Нетрудно проверить, что X и Y , найденные по формулам (6) , являются решением уравнения (3). Аналогичные формулы имеют место и для систем N линейных уравнений с N неизвестными. Способ нахождения решений уравнения (3) по формулам (6) называется Правилом Крамера. Г. Крамер (1704-1752) швейцарский математик, заложил основы теории определителей.
Пусть дана квадратная матрица A порядка N:
 .
.
Определение 8. Определителем n-го порядка или Определителем квадратной матрицы порядка N называется алгебраическая сумма всевозможных произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы со знаком равным знаку подстановки, первая строка которой составлена из номеров строк, а вторая строка составлена из номеров столбцов, из которых взяты элементы, входящие в произведение.
Обозначается определитель n-го порядка одним из следующих способов:
 .
.
По определению ![]() алгебраическая сумма произведений вида:
алгебраическая сумма произведений вида:
![]() , (7)
, (7)
Где индексы ![]() образуют некоторую перестановку из чисел 1,2,...,N. Так как по теореме 1 имеется N! перестановок из n элементов, то определитель алгебраическая сумма N! произведений вида (7). Для вычисления знака произведения составим подстановку
образуют некоторую перестановку из чисел 1,2,...,N. Так как по теореме 1 имеется N! перестановок из n элементов, то определитель алгебраическая сумма N! произведений вида (7). Для вычисления знака произведения составим подстановку

И знак произведения (7) будет равен знаку подстановки ![]() . Поэтому в символьном виде определитель можно записать так:
. Поэтому в символьном виде определитель можно записать так:
![]() , (8)
, (8)
Где суммирование ведется по всем N! подстановкам N-й степени.
Покажем, что определитель 2-го порядка вычисляется по формуле:
![]() . (9)
. (9)
Действительно, по определению он равен алгебраической сумме 2!, т. е. 2-х произведений ![]() . Знаки этих произведений равны соответственно знакам подстановок:
. Знаки этих произведений равны соответственно знакам подстановок:
![]() ,
,
Т. е. 1 и -1, что совпадает с их знаками в формуле (9).
Покажем, что определитель 3-го порядка вычисляется по формуле:
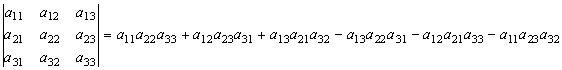 . (10)
. (10)
Действительно, по определению он равен алгебраической сумме 3!, т. е. 6-ти произведений
![]() .
.
Знаки этих произведений равны соответственно знакам подстановок:
![]() .
.
Эти подстановки имеют соответственно 0, 2, 2, 3, 1, 1 инверсий и знаки их соответственно равны 1, 1, 1, -1, -1, -1, что совпадает с их знаками в формуле (10).
Знаки в формулах (9) и (10) снабжаются по правилам, которые описываются следующими схемами.![]()
![]()
![]()
![]()
При n=2 и n=3

На этих рисунках соединены линиями элементы матрицы, составляющие произведения определителя, входящие в него со знаком + и -.
Пример 5.
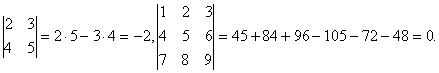
| < Предыдущая | Следующая > |
|---|