Ответы
Глава 1
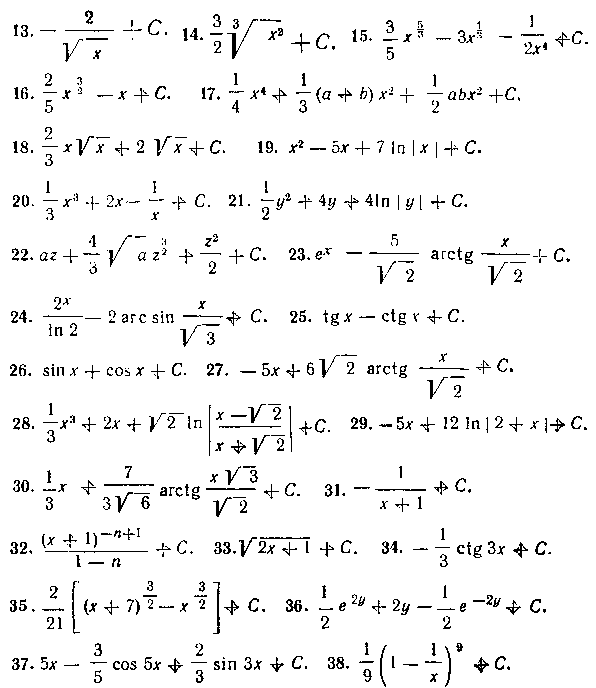
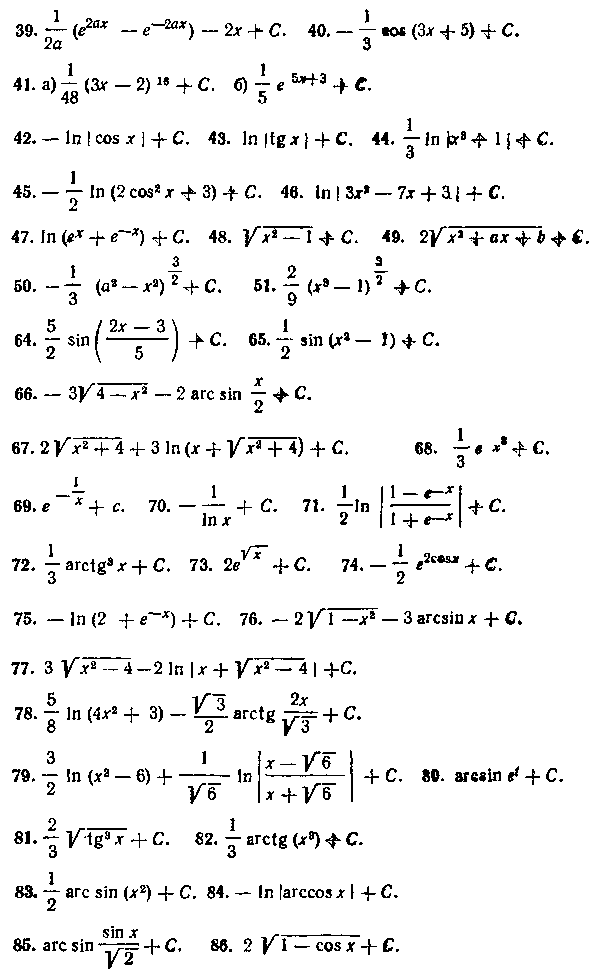
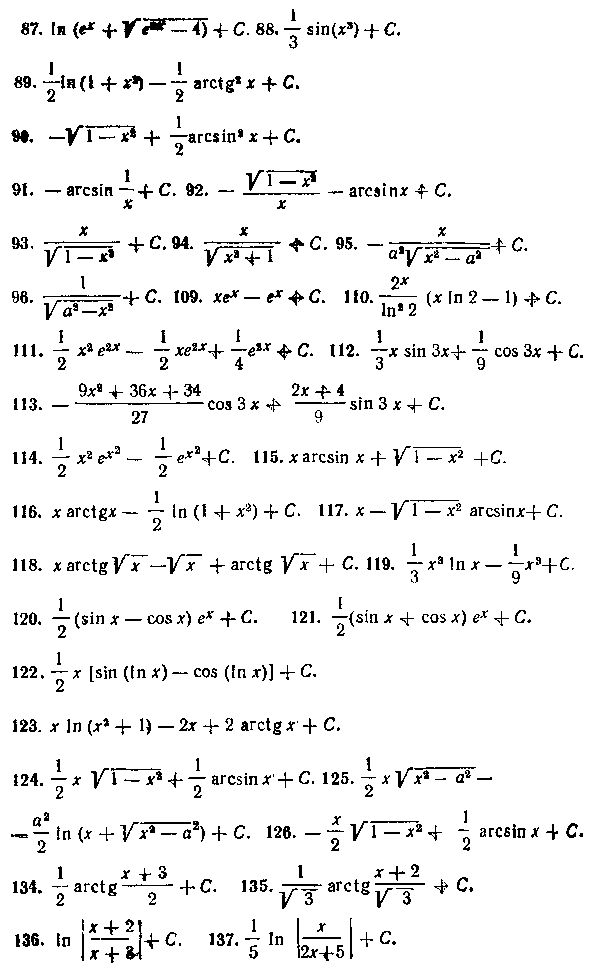
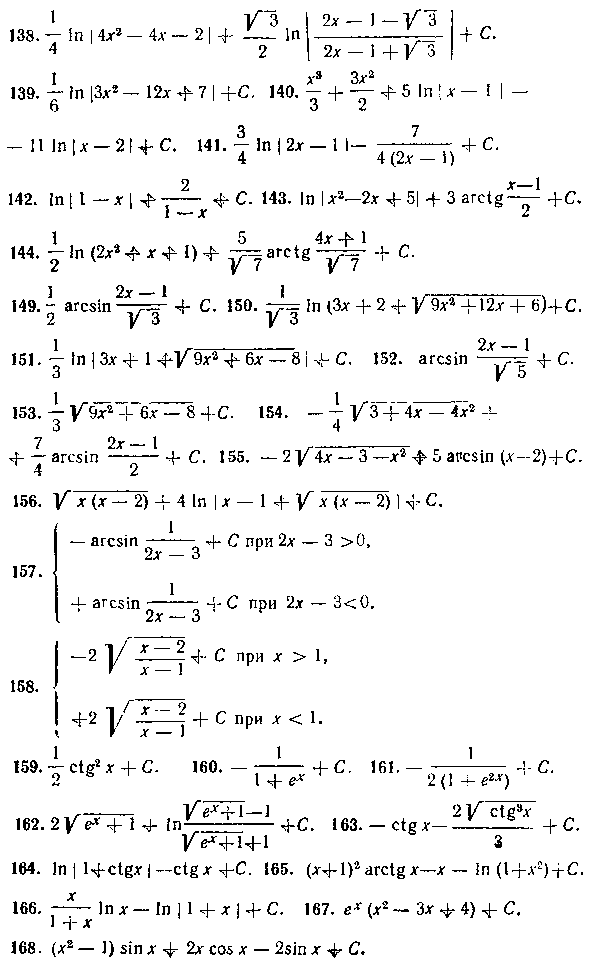

Глава II 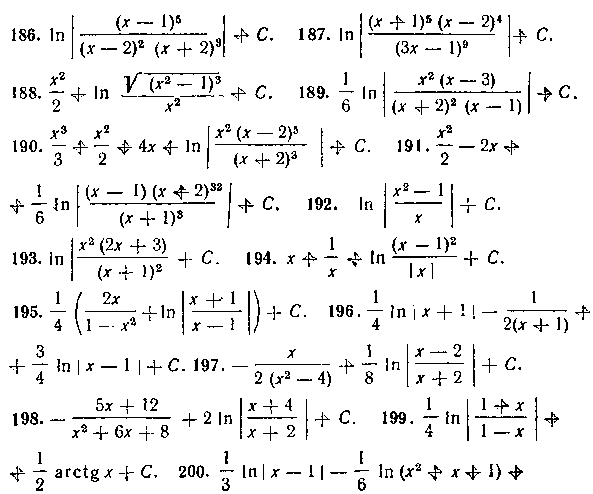

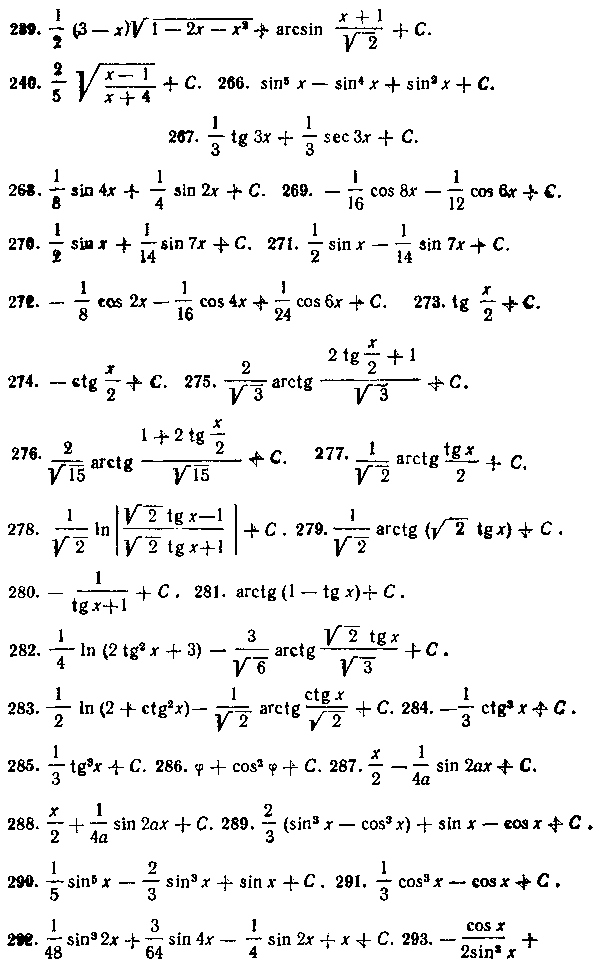

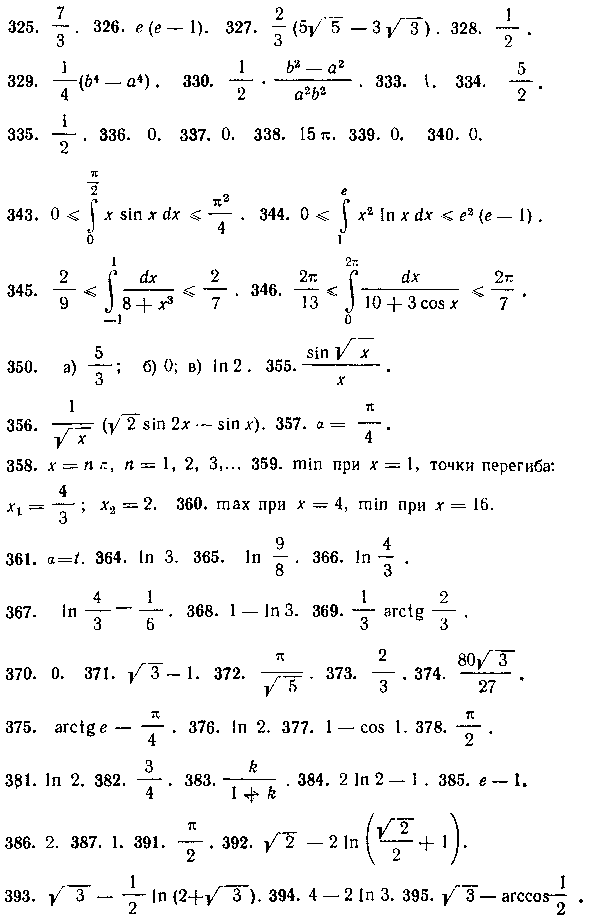
325. — . 326. е(е— I). 327. -(5/5 — 3/ 3). 328. —.
329. —(6« — а«). 330. — •-——. 333. I. 334. —
335. ? 336. 0. 337. 0. 338. 15 тс. 339. 0. 340. 0.
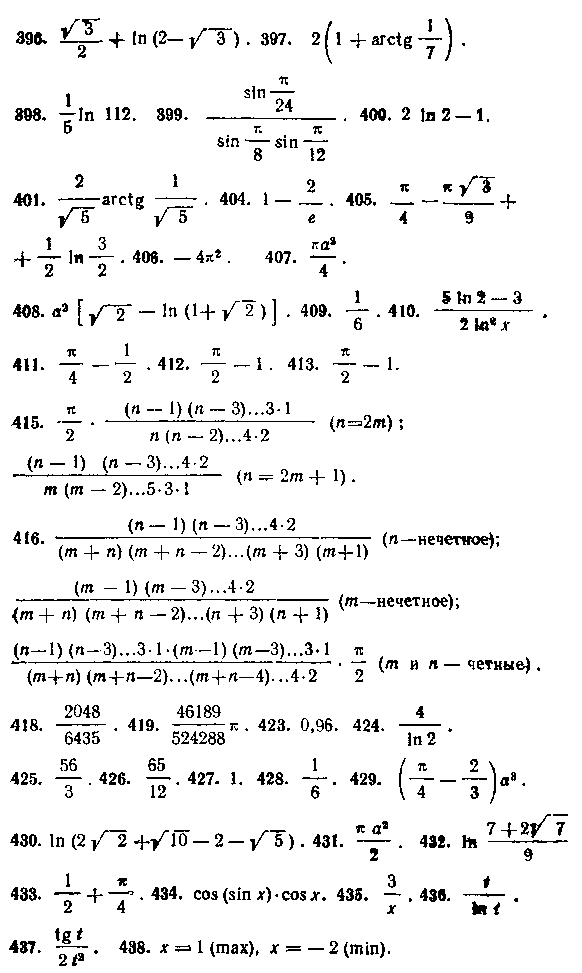

Глава IV

Ж

ОГЛАВЛЕНИЕ
ПЕРВООБРАЗНАЯ ФУНКЦИЯ (НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ)
Глава /. Основные способы интегрирования
§ I. Способ непосредственного интегрирования * , . . 5 § 2. Способ замены переменной (способ подстановки) . 14 § 3. Способ интегрирования почастям........ 23
Глава II. Основные классы интегрируемых функций
§ I. Интегрирование рациональных функций, , , , 43 § 2. Интегрирование некоторых выражений, содержащих
§ 3. Интегрирование биномиальных дифференциалов, , 63
§ 4. Подстановки Эйлера...........% 66
§ 5. Интегрирование выражений, содержащих тригонометрические функции. . ..................70
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Глава III. Вычисление определенных интегралов
§ I. Вычисление непосредственным суммированием. , , 91 § 2* Вычисление определенных интегралов с помощью
первообразных. Применение к вычислению рядов. 107 § 3. Замена переменной. Интегрирование по частям. .116 § 4. Приближенное интегрирование, * 125
§ I. Вычисление площадей. . 130
§ 2. Длина дуги плоской кривой. . * 145
§ 3. Объем тела произвольной формы. , . , * . * 149
§ 4. Объемы? поверхности тел вращения **»«*. 151
Глава V. Приложения к вопросам физики
§ I. Вычисление статических моментов и моментов инерции 164 § 2. Вычисление координат центра тяжести плоских кривых и плоских тел. Теорема Гюльдена...... 172
§ 3. Разные задача............., . 180
Ответы, . . . t f. , i 185
| < Предыдущая |
|---|
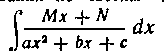 .......31
.......31 ......39
......39