6.2.3. Интегральная теорема Лапласа

Если вероятность p наступления события А в каждом из n независимых испытаний постоянна и отлична от 0 и 1, то вероятность того, что m — число появлений события А при n испытаниях — заключено между удовлетворяет соотношению:

(4)

функция Лапласа, а и

приближенное равенство:

Отсюда при достаточно большом n следует

Если в соотношении (4) положить

то получим

При достаточно больших n из формулы (6) следует приближенное равенство:

или

/ \

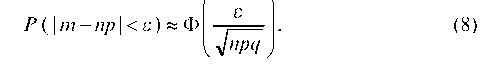
Пример 6.18. При установившемся технологическом процессе фабрика выпускает в среднем 70% продукции первого сорта. Чему равна вероятность того, что в партии из 1000 изделий число первосортных заключено между 652 и 760?

Решение. Известны число независимых испытаний n = 1000 и вероятность наступления события в отдельном испытании p = 0,7. Требуется найти вероятность того, что число появлений события заключено между a = 652 и b = 760. Искомую вероятность находим по формуле (5)

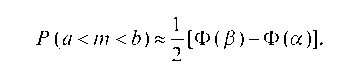
Пример 6.19. Бюффон бросил монету 4040 раз, причем герб выпал 2048 раз. Можно ли считать полученное отклонение числа появлений герба от 2020 случайным или же оно обусловлено систематической причиной?

Решение. Расхождение эмпирической частоты Бюффона от теоретической можно считать случайным, если вероятность того, что при 4040 бросаниях монеты отклонение числа выпадений герба от 2020 равно или больше по абсолютной величине, чем у Бюф-фона, достаточно большая. Пусть m — число выпадений герба при 4040 бросаниях монеты. Находим вероятность:

Поэтому искомая вероятность приближенно равна:

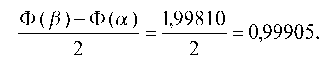
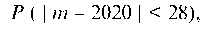
где

с

\

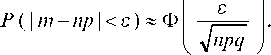
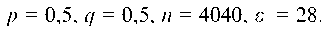
В данном случае. Отсюда

Поэтому вероятность противоположного события, т. е. того, что | m - 2020 | > 28, равна 1 - 0,6217 = 0,3783. Так как эта вероятность достаточно большая, то результат Бюффона можно считать обусловленным случайными причинами.

Пример 6.20. Посажено 600 семян кукурузы с вероятностью

0,9 прорастания для каждого семени. Найти границу абсолютной величины отклонения частости взошедших семян от вероятности р = 0,9, если эта граница должна быть гарантирована с вероятностью P = 0,995.

Решение. Мы знаем, что если n — число независимых испытаний и р — вероятность наступления события в отдельном испытании, то при любом s > 0 имеет место приближенное равенство:

где q = 1 - р. В нашем случае n = 600, р = 0,9 , q = 1 - 0,9 = 0,1, P = 0,995, e — ? По формуле (7):

Пользуясь таблицей, решаем уравнение Ф (t) = 0,995; t = 2,81.

Отсюда e и, следовательно,

Пример 6.21. С конвейера сходит в среднем 85% изделий первого сорта. Сколько изделий необходимо взять, чтобы с вероятностью 0,997 отклонение частости изделий первого сорта в них от

0,85 по абсолютной величине не превосходило 0,01?

Решение. Здесь p = 0,85, q = 1 - 0,85 = 0,15, e = 0,01, P = 0,997,

известна

n — ? Так как в равенстве I

вероятность P, стоящая слева, то сначала решим уравнение Ф (t) = P.

Пусть tP — корень этого уравнения. Тогда

и, следовательно,

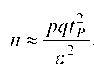
. Для нашего случая t0997 = 3, поэтому

< Предыдущая		Следующая >