Вариант № 30

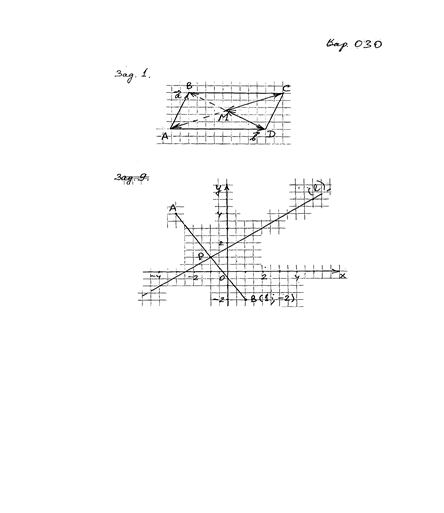
Задача 1(см. рис. 1)

1)

2)

Задача 2

Пусть , т. е. ; след. вектор .

Задача 3

Рассм. векторы

;

;

Вычислим ;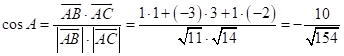

;

;

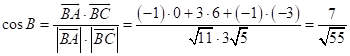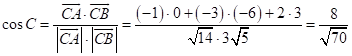Имеем , след., углы Острые, а угол - тупой

И след., - наибольший внутренний угол ; .

Задача 4

Рассм. вектор ;

Пусть искомый вектор ; тогда по усл. задачи должны выполняться след. рав–ва: ;

;

;

; искомый вектор .

Задача 5

Угол между векторами Определим из равенства: ;

Вычислим

;

Рассм. ;

;

; .

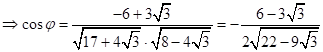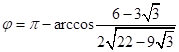Задача 6

1) , где ; ;

;

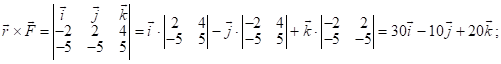
2) ;

Направл. косинусы вектора : ; ; .

Задача 7

Пусть ;

; ;

Решим с-му ур-й (1) – (3) и опр-м координаты вектора :

;

;

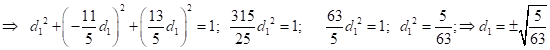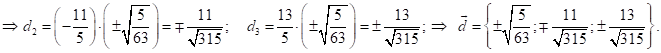
Задача 8

Пусть искомая вершина тетраэдра (т. к. т.) ;

Рассм. в-ры: ;

Рассм. смешанное произв-е:

;

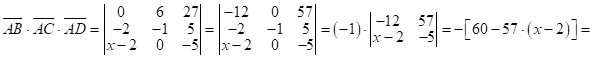
Рассм. объём тетраэдра : ; ; ; ; ; ;

След., возможные положения искомой т. : ; .

Задача 9

Найти точку , симметричную точке Относительно прямой .

Рассмотрим один из нормальных векторов прямой ; его можно взять в качестве направляющего вектора прямой и записать уравнение прямой в виде:

или определим координаты точки пересечения прямых

И : ;

Определим теперь координаты искомой точки из условия, что т. есть середина отрезка :

.

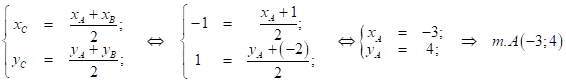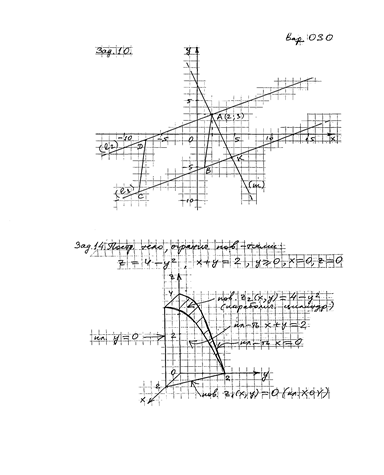
Задача 10

Определить высоту параллелограмма, если две его стороны лежат на прямых и .

Очевидно, высота данного параллелограмма равна расстоянию между параллельными прямыми и ;

Рассм. нормальный вектор Прямой ( или );

Рассм. т. и т. ; рассм. вектор ;

Искоиое расстояние равно модулю проекции вектора на направление вектора :

Вычислим ;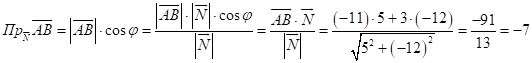

.

Задача 11

Составить уравнение плоскости, проходящей через точку перпендикулярно к двум плоскостям: .

Пусть - искомая плоскость; рассм. норм. векторы

Рассм. норм. вектор ;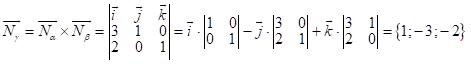

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

.

Задача 12

Составить канонические и параметрические уравнения прямой , заданной как пересечение двух

Плоскостей: .

Рассм. норм. векторы ; рассм. направл. вектор прямой : ;

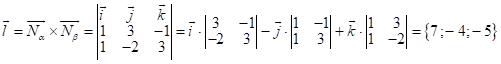Определим какую-либо точку ; рассм.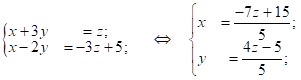

Положим , тогда ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т.

Параллельно вектору : ; параметрические ур-я прямой :

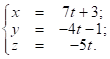
Задача 13

Составить уравнение плоскости , проходящей через точку Параллельно двум прямым

Рассм. направл. векторы прямых: ;

, След. в качестве нормального вектора плоскости можно взять вектор ;

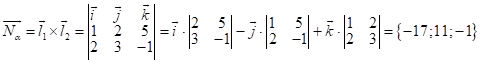Составим теперь уравнение плоскости как плоскости с нормальным вектором , проходящей через точку : рассм. произв. т. и рассм. вектор ; ,

Т. е. ; .

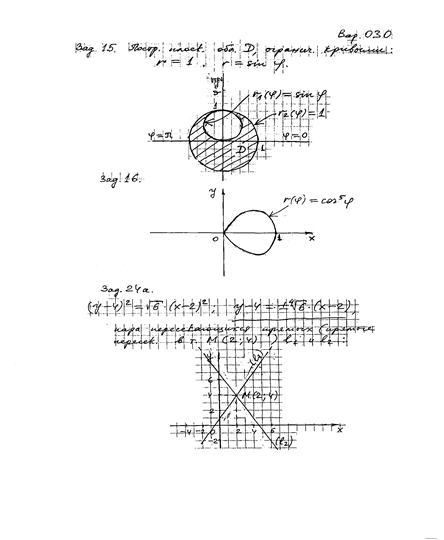
Задача 16

Перейти в уравнении к полярным координатам и построить кривую: .

Перейдём к полярным координатам по формулам:

Уравнение кривой Примет вид:

Задача 17

1) вычисление определителя 3-го порядка: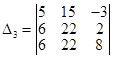

A) Непосредственное вычисление (по правилу треугольников):

Б) разложение по 3-му столбцу:

2)вычисление определителя 4-го порядка:

.

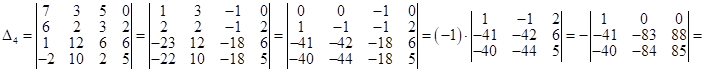
Задача 18

Запишем данную систему уравнений в матричной форме:

, (1) , где ; ; ;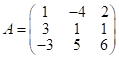

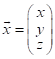Рассм. опред-ль матрицы : ,

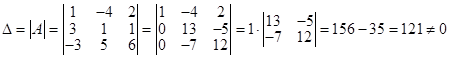След., матр. - невырожденная и можно применять формулы Крамера и вычислять обратную

Матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул:

, , , где ,

;

;

;

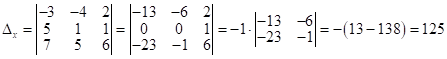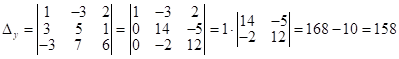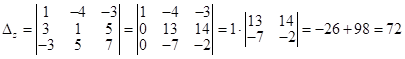Реш–е с–мы ур–й (1) в коорд. форме: , , ;

Вектор–решение с-мы (1): ;

2)получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.- невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : , ;

Вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

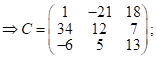транспонируем м-цу и получим «присоединённую» м-цу ;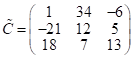

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

;

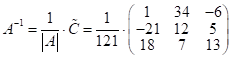Находим теперь вектор-решение: ;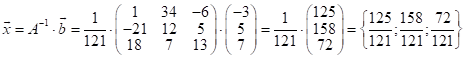

3) решим с – му ур – й (1) методом Гаусса:

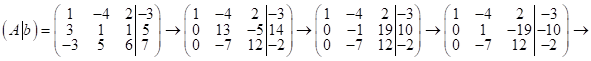
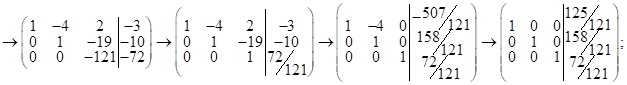
Решение системы в коорд. форме:

Задача 19

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

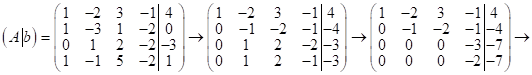
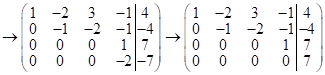; Имеем ;

Так как , то по теореме Кронекера - Капелли данная система ур-й несовместна.

Задача 20

Запишем данные преобразования в матричной форме: , где матрицы

И вектор - столбцы имеют вид:

;

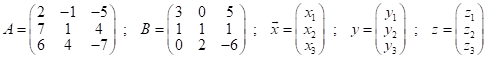Рассм. ;

Вычислим матрицу .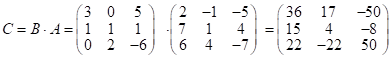

Задача 21

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

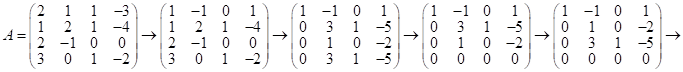
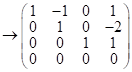; ранг матрицы , след. данная система векторов линейно зависима.

Задача 23

Задан многочлен ;

А) найти корни многочлена;

Б) разложить многочлен по корням;

В) разложить многочлен на множители только с действительными коэффициентами.

А) ; разделим На :

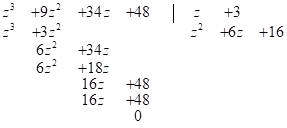
Рассм. теперь ур – е ; ;

Б) разложение многочлена на линейные множители:

;

Разложение многочлена на множители только с действительными коэффициентами:

.

Задача 24(а)

Установить вид и построить линию, заданную уравнением:

.

;

; ; , - пара пересекающихся прямых (прямые пересекаются

В точке ) .

Задача 25

Привести уравнение поверхности 2-го порядка к каноническому виду, определить вид поверхности.

;

;

;

; ;

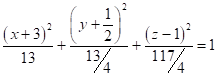Перейдём к новым координатам по формулам: ;

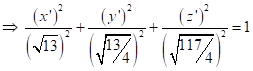, - эллипсоид с центром в точке

И полуосями .

Задача 26

.

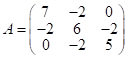1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

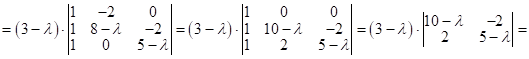
- собств. значения (действ. и различные ) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм.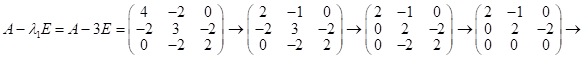

;

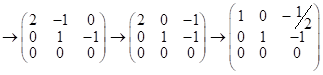Рассм. 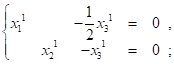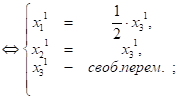Пусть , тогда вектор ;

Б) рассм.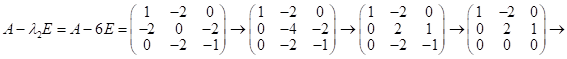

;

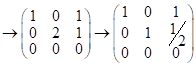Рассм.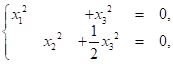

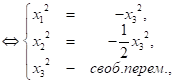
Пусть , тогда вектор ;

В) рассм.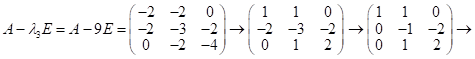

;

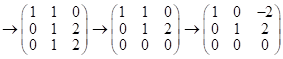рассм.

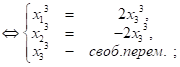
Пусть , тогда вектор ;

След., собств. векторы линейного преобразования суть:

; ; .

< Предыдущая