Вариант № 23
1. Исследовать числовой ряд на сходимость: ![]() .
.
Так как ![]() , то
, то ![]() . Ряд
. Ряд ![]() сходится, так как ряд с общим членом
сходится, так как ряд с общим членом ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() . В данном случае
. В данном случае ![]() . Следовательно, сходится и ряд с общим членом
. Следовательно, сходится и ряд с общим членом ![]() по первому признаку сравнения. Ответ: Ряд сходится.
по первому признаку сравнения. Ответ: Ряд сходится.
2. Исследовать числовой ряд на сходимость: ![]() .
.
Применим признак д, Аламбера:
 .
.
Следовательно, данный ряд сходится. Ответ: Ряд сходится.
3. Исследовать числовой ряд на сходимость: ![]() .
.
Имеем ![]() . Функция
. Функция ![]() удовлетворяет условиям интегрального признака Коши. Действительно,
удовлетворяет условиям интегрального признака Коши. Действительно, ![]() монотонно убывает на
монотонно убывает на ![]() и, следовательно, интеграл
и, следовательно, интеграл 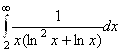 и исходный ряд сходятся или расходятся одновременно. Имеем
и исходный ряд сходятся или расходятся одновременно. Имеем 
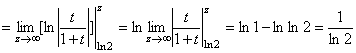 . Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.
. Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.
4. Исследовать ряд на абсолютную или условную сходимость: ![]() .
.
Исходный ряд является знакочередующимся рядом и удовлетворяет всем условиям теоремы Лейбница. Действительно, по абсолютной величине члены ряда монотонно убывают, а общий член ряда по абсолютной величине стремится к нулю. Рассмотрим ряд ![]() . Очевидно, что
. Очевидно, что ![]() . Ряд с общим членом
. Ряд с общим членом ![]() сходится по признаку сравнения в предельной форме со сходящимся рядом
сходится по признаку сравнения в предельной форме со сходящимся рядом ![]() . Тогда сходится и ряд с общим членом
. Тогда сходится и ряд с общим членом ![]() по первому признаку сравнения. Ответ: Ряд сходится абсолютно.
по первому признаку сравнения. Ответ: Ряд сходится абсолютно.
5. Определить область сходимости функционального ряда:  .
.
Очевидно, что  . Если ряд с общим членом
. Если ряд с общим членом  сходится, то сходится и данный ряд по первому признаку сходимости. Применим радикальный признак Коши к ряду
сходится, то сходится и данный ряд по первому признаку сходимости. Применим радикальный признак Коши к ряду  :
:
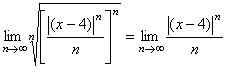 . Если
. Если ![]() , то можно применить правило Лопиталя:
, то можно применить правило Лопиталя: ![]() . При
. При ![]() получим:
получим: 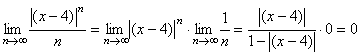 . Здесь применена формула для бесконечно убывающей геометрической прогрессии. Итак, ряд сходится, если
. Здесь применена формула для бесконечно убывающей геометрической прогрессии. Итак, ряд сходится, если ![]() , т. е.
, т. е. ![]() . Или
. Или ![]() . Следовательно, интервал
. Следовательно, интервал ![]() является интервалом сходимости данного ряда. Исследуем ряд на концах интервала. При
является интервалом сходимости данного ряда. Исследуем ряд на концах интервала. При ![]() получим знакочередующийся числовой ряд
получим знакочередующийся числовой ряд ![]() , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При ![]() получим числовой ряд
получим числовой ряд ![]() , который сходится по признаку сравнения со сходящимся рядом
, который сходится по признаку сравнения со сходящимся рядом ![]() (бесконечно убывающая геометрическая прогрессия). Действительно,
(бесконечно убывающая геометрическая прогрессия). Действительно, ![]() , начиная с
, начиная с ![]() . Ответ: Областью сходимости ряда является множество
. Ответ: Областью сходимости ряда является множество ![]()
6. Определить область сходимости функционального ряда: ![]() .
.
Применим признак д, Аламбера к ряду 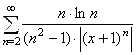 :
: 
![]() . Последний предел вычисляется пол правилу Лопиталя:
. Последний предел вычисляется пол правилу Лопиталя: ![]() . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: ![]() , т. е.
, т. е. ![]() или
или ![]() . Следовательно, ряд сходится при
. Следовательно, ряд сходится при ![]() и
и ![]() . Исследуем ряд на концах интервала. При
. Исследуем ряд на концах интервала. При ![]() получим числовой ряд
получим числовой ряд ![]() , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При ![]() получим числовой ряд
получим числовой ряд ![]() . Этот ряд расходится по признаку сравнения с гармоническим рядом. Действительно,
. Этот ряд расходится по признаку сравнения с гармоническим рядом. Действительно, ![]() . Ответ: Областью сходимости ряда является множество
. Ответ: Областью сходимости ряда является множество ![]()
7. Определить область сходимости функционального ряда: ![]() .
.
Поскольку всегда ![]() , то достаточно рассмотреть ряд
, то достаточно рассмотреть ряд  с положительными членами. Применим признак д, Аламбера:
с положительными членами. Применим признак д, Аламбера: 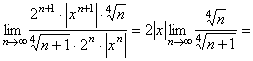
![]() . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: ![]() , т. е.
, т. е. ![]() . Следовательно, ряд сходится при
. Следовательно, ряд сходится при ![]() . Исследуем ряд на концах интервала. При
. Исследуем ряд на концах интервала. При ![]() получим числовой ряд
получим числовой ряд ![]() (здесь применена формула
(здесь применена формула ![]() . Этот ряд расходится, так как степень в знаменателе меньше единицы. При
. Этот ряд расходится, так как степень в знаменателе меньше единицы. При ![]() получим числовой ряд
получим числовой ряд ![]() (здесь применена формула
(здесь применена формула ![]() . Этот ряд сходится по признаку Лейбница. Ответ: Областью сходимости ряда является множество
. Этот ряд сходится по признаку Лейбница. Ответ: Областью сходимости ряда является множество ![]() .
.
8. Разложить указанную функцию в ряд Тейлора по степеням ![]() . Указать область сходимости:
. Указать область сходимости: ![]() .
.
Воспользуемся известным разложением функции ![]() :
:
![]() . Этот ряд сходится при
. Этот ряд сходится при ![]() . Преобразуем исходную функцию:
. Преобразуем исходную функцию: ![]() . В записанном выше разложении логарифмической функции положим
. В записанном выше разложении логарифмической функции положим ![]() , получим:
, получим: ![]() Или
Или ![]() . Ряд сходится при
. Ряд сходится при ![]() или
или ![]() .
.
Ответ: ![]() .
.
9. Указанную функцию разложить в ряд Маклорена, используя разложения в ряд функций ![]() указать область сходимости:
указать область сходимости: ![]() .
.
Воспользуемся разложением функции ![]() в ряд Маклорена:
в ряд Маклорена: ![]() . Этот ряд сходится при
. Этот ряд сходится при ![]() . Тогда
. Тогда ![]() (здесь учтено, что
(здесь учтено, что ![]() ). Областью сходимости ряда будет
). Областью сходимости ряда будет ![]() . Ответ:
. Ответ: ![]() ,
, ![]() .
.
10. Вычислить приближённо с точностью до 10-4:  .
.
Воспользуемся формулой ![]() . Получим
. Получим ![]() . Тогда
. Тогда 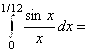
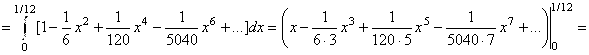
![]() . В соответствии с теоремой Лейбница заданная точность будет достигнута, если первое отбрасываемое слагаемое будет по абсолютной величине меньше, чем
. В соответствии с теоремой Лейбница заданная точность будет достигнута, если первое отбрасываемое слагаемое будет по абсолютной величине меньше, чем ![]() . В данном случае
. В данном случае ![]() . Очевидно, что
. Очевидно, что ![]() . Следовательно, достаточно взять одно слагаемое:
. Следовательно, достаточно взять одно слагаемое:  . Ответ:
. Ответ: 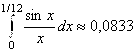 (Ответ в методичке дан для интеграла
(Ответ в методичке дан для интеграла 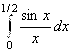 , Что противоречит условию задачи).
, Что противоречит условию задачи).
11. Вычислить предел, используя разложение функций в ряд Тейлора: ![]() .
.
Так как ![]() и
и ![]() , то
, то ![]() и
и ![]() . Следовательно,
. Следовательно,
![]()
![]() .
.
Ответ: ![]() .
.
12. Найти сумму ряда:![]() .
.
Обозначим сумму ряда через S(X). Тогда ![]()
![]() . Но
. Но ![]() есть сумма бесконечно убывающей геометрической прогрессии при
есть сумма бесконечно убывающей геометрической прогрессии при ![]() . Следовательно,
. Следовательно, 

![]() . Ответ:
. Ответ: ![]() .
.
13. Найти сумму ряда:![]() .
.
Обозначим сумму ряда через S(X). Тогда ![]()
![]() .
. 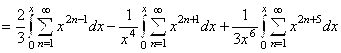 Но
Но ![]() есть суммы бесконечно убывающих геометрических прогрессий при
есть суммы бесконечно убывающих геометрических прогрессий при ![]() . Следовательно,
. Следовательно, 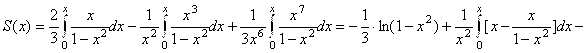
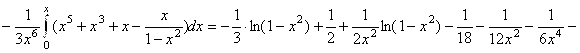
![]() .
.
Ответ: ![]() .
.
14. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: ![]()
Будем искать решение уравнения в виде ![]() , где
, где ![]() . Будем последовательно вычислять производные
. Будем последовательно вычислять производные ![]() :
: ![]() ,
, ![]()
![]() . Следовательно,
. Следовательно, ![]()
![]() . Таким образом,
. Таким образом, ![]() .
.
Ответ: ![]() .
.
15. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: ![]()
Ищем решение уравнения в виде ![]() . Тогда
. Тогда ![]() . Подставляя это в исходное уравнение, получим:
. Подставляя это в исходное уравнение, получим: ![]() . Первую сумму можно записать в следующем виде:
. Первую сумму можно записать в следующем виде: ![]() . Вторую сумму в уравнении можно записать виде:
. Вторую сумму в уравнении можно записать виде: ![]() . Тогда
. Тогда ![]() . Объединим обе суммы, выделяя «лишние» слагаемые:
. Объединим обе суммы, выделяя «лишние» слагаемые: ![]() . Это равнество должно выполняться для различных значений X. Это возможно лишь тогда, когда коэффициенты при всех степенях X будут равны нулю, т. е.
. Это равнество должно выполняться для различных значений X. Это возможно лишь тогда, когда коэффициенты при всех степенях X будут равны нулю, т. е. ![]() и
и ![]() . Отсюда получаем рекуррентную формулу:
. Отсюда получаем рекуррентную формулу: ![]() Следовательно,
Следовательно, ![]()
![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() . Получим:
. Получим: ![]()
![]()
![]() . Таким образом,
. Таким образом, ![]()
![]() . Ответ:
. Ответ:
![]() .
.
16. Разложить заданную графиком периодическую функцию в ряд Фурье:
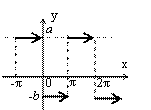 По графику определяем
По графику определяем ![]() .
.
Разложение функции в ряд Фурье имеет вид: ![]() . Вычислим коэффициенты
. Вычислим коэффициенты ![]() :
: 
 . Если
. Если ![]() чётное, то
чётное, то ![]() и
и ![]() , если
, если ![]() нечётное. Положим
нечётное. Положим ![]() . Для нечётных
. Для нечётных ![]() получим
получим ![]() Вычислим коэффициенты
Вычислим коэффициенты ![]() :
: 
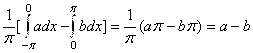 . Таким образом,
. Таким образом, ![]() .
.
Ответ: ![]() .
.
17. Разложить функцию в ряд Фурье на ![]() :
: ![]()
Функция ![]() является нечётной. Поэтому в её разложении в ряд Фурье
является нечётной. Поэтому в её разложении в ряд Фурье ![]() все коэффициенты
все коэффициенты ![]() . Вычислим коэффициенты
. Вычислим коэффициенты ![]() :
: 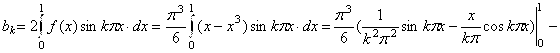

![]() Таким образом,
Таким образом, ![]() .
.
Ответ: ![]() .
.
18. Найти разложение функции ряд Фурье в комплексной форме на ![]() :
: ![]() .
.
В комплексной форме ряд Фурье функции ![]() периода
периода ![]() имеет вид:
имеет вид: 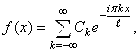 где
где  . В данном случае
. В данном случае 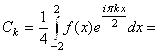

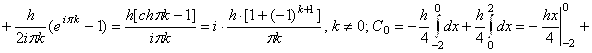
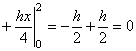 . Таким образом,
. Таким образом, 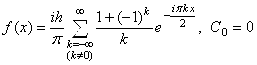 . Ответ:
. Ответ:  .
.
19. Функцию ![]() представить интегралом Фурье в действительной форме:
представить интегралом Фурье в действительной форме:
![]() .
.
Представление функции интегралом Фурье в действительной форме имеет вид 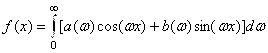 , где
, где 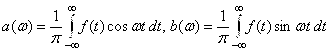 . Функция является нечётной, поэтому и
. Функция является нечётной, поэтому и ![]() , найдём
, найдём ![]() :
: 
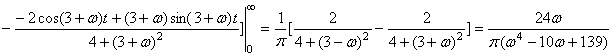 . Таким образом,
. Таким образом,  .
.
Ответ:  .
.
20. Функцию ![]() представить интегралом Фурье в комплексной форме:
представить интегралом Фурье в комплексной форме:
![]() .
.
Представление функции интегралом Фурье в комплексной форме имеет вид  , где
, где 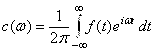 . Вычислим
. Вычислим ![]() :
: 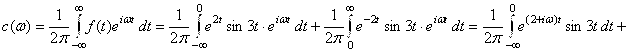
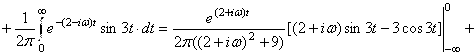

![]() . Таким образом,
. Таким образом,  . Ответ:
. Ответ: 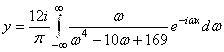
| < Предыдущая | Следующая > |
|---|