Вариант № 06
1. Найти область определения функции: ![]() .
.
Область определения данной функции определяется неравенством ![]() , т. е.
, т. е. ![]() . Далее, знаменатель не должен обращаться в нуль:
. Далее, знаменатель не должен обращаться в нуль: ![]() или
или ![]() . Кроме того, аргумент логарифма не может быть нулём:
. Кроме того, аргумент логарифма не может быть нулём: ![]() . Объединяя результаты, получим:
. Объединяя результаты, получим: ![]() . Ответ:
. Ответ: ![]() .
.
 2. Построить график функции:
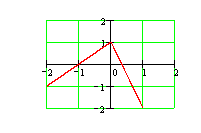
2. Построить график функции: ![]() .
.
Данная функция определена на всей числовой оси. Преобразуем функцию: если ![]() , то
, то ![]() . Если
. Если ![]() , то
, то ![]() .
.
Таким образом, ![]() .
.
Ответ: график представлен на рисунке.
3. Построить график функции: ![]()
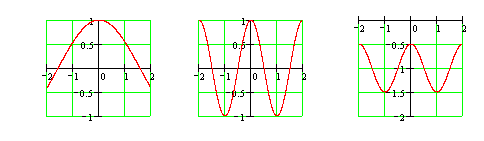
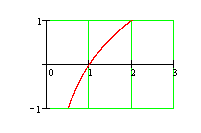
Данная функция определена на всей числовой оси. Последовательно строим сначала ![]() , затем
, затем ![]() («сжимая» график в π раз по оси ОХ), затем уменьшаем значения функции в 0,5 раза и от полученного значения отнимаем единицу, т. е «сжимаем» график по оси OY в два раза и опускаем весь график на единицу ниже. Ответ: построения представлены на рисунках.
(«сжимая» график в π раз по оси ОХ), затем уменьшаем значения функции в 0,5 раза и от полученного значения отнимаем единицу, т. е «сжимаем» график по оси OY в два раза и опускаем весь график на единицу ниже. Ответ: построения представлены на рисунках.
 4. Построить график функции:
4. Построить график функции: 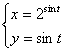
Исключим параметр T: ![]() или
или ![]() . Функция определена только для
. Функция определена только для ![]() , так как
, так как ![]() всегда. Это часть графика логарифмической функции с двоичным основанием. Ответ: График представлен на рисунке.
всегда. Это часть графика логарифмической функции с двоичным основанием. Ответ: График представлен на рисунке.
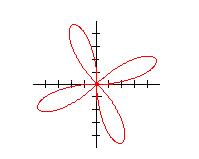
5. Построить график функции: ![]() .
.
 Поскольку
Поскольку ![]() , то функция существует для тех значений φ, для которых
, то функция существует для тех значений φ, для которых ![]() . Это наблюдается при
. Это наблюдается при ![]() или
или ![]() . Полагая
. Полагая ![]() , получаем четыре интервала:
, получаем четыре интервала: ![]() ,
, ![]() ,
, ![]() и
и ![]() . В каждом интервале функция возрастает от 0 до 1, затем убывает от 1 до 0. Получаем четырёхлепестковую «розу». Ответ: График представлен на рисунке.
. В каждом интервале функция возрастает от 0 до 1, затем убывает от 1 до 0. Получаем четырёхлепестковую «розу». Ответ: График представлен на рисунке.
6. Вычислить предел: ![]() .
.
Воспользуемся формулой для суммы арифметической прогрессии: ![]() . Аналогично,
. Аналогично, ![]() . Тогда
. Тогда ![]() .
.
Ответ: ![]() .
.
7. Вычислить предел: ![]() (неопределённость вида (0/0)).
(неопределённость вида (0/0)).
Разлагаем числитель и знаменатель на простые множители: ![]()
![]() . Ответ:
. Ответ: ![]() .
.
8. Вычислить предел: ![]() (неопределённость вида (0/0)).
(неопределённость вида (0/0)).
Вычислим предел, используя замену переменной: 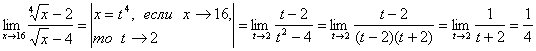 .
.
Ответ: ![]() .
.
9. Вычислить предел: ![]() (неопределённость вида (0/0)).
(неопределённость вида (0/0)).
Воспользуемся первым замечательным пределом: ![]() :
:
![]()
![]()
![]() . Ответ:
. Ответ: ![]() .
.
10. Вычислить предел:  (неопределённость вида (1∞)).
(неопределённость вида (1∞)).
Приведём предел ко второму замечательному пределу: ![]() :
: 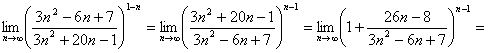
 .
.
Ответ: 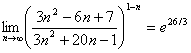 .
.
11. Вычислить предел: 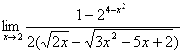 (неопределённость вида (0/0)).
(неопределённость вида (0/0)).
Умножим на сопряжённое выражение:
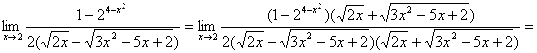
![]()
![]() ~
~![]()
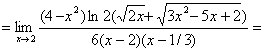
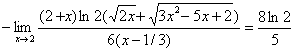 .
.
Ответ: 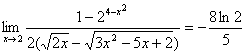 .
.
12. Исследовать функцию на непрерывность и построить эскиз графика: ![]() .
.
Область определения – все действительные числа, кроме X=−1. В точке X=−1 функция имеет разрыв, во всех других точках является непрерывной (как элементарная функция). Исследуем поведение функции в окрестности точки разрыва: 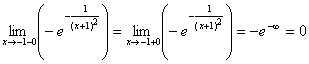 .
.  Таким образом, в точке X=−1 имеют место устранимый разрыв. Полагая
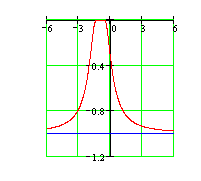
Таким образом, в точке X=−1 имеют место устранимый разрыв. Полагая ![]() , можно считать функцию непрерывной на всей числовой оси. Для построения эскиза графика функции рассмотрим поведение функции в бесконечности:
, можно считать функцию непрерывной на всей числовой оси. Для построения эскиза графика функции рассмотрим поведение функции в бесконечности: 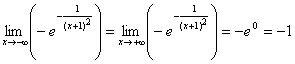 . Ответ: В точке X=−1 функция имеет устранимый разрыв, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
. Ответ: В точке X=−1 функция имеет устранимый разрыв, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
13. Исследовать функцию на непрерывность и построить эскиз графика: 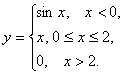 .
.
 Область определения функции:
Область определения функции: ![]() . Ось ОХ разбивается на три интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций. Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
. Ось ОХ разбивается на три интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций. Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
![]()
![]()
![]() . Таким образом, в точке X=0 функция непрерывна, а в точке X=2 функция терпит разрыв первого рода. Величина скачка функции в точке X=2 равна -2.
. Таким образом, в точке X=0 функция непрерывна, а в точке X=2 функция терпит разрыв первого рода. Величина скачка функции в точке X=2 равна -2.
Ответ: В точке X=2 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
14. Исходя из определения производной, найти ![]() :
:
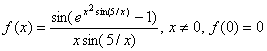 .
.
По определению ![]() . Заменим ΔX на X-X0:
. Заменим ΔX на X-X0:
![]() . Но
. Но ![]() , поэтому
, поэтому ![]() . В данном случае
. В данном случае 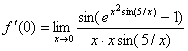 . Но Sin(T) ~T, а Et-1~T при T→0 . Поэтому
. Но Sin(T) ~T, а Et-1~T при T→0 . Поэтому
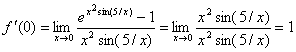 . Ответ:
. Ответ: ![]()
15. Найти производную показательно-степенной функции: ![]() . Прологарифмируем функцию:
. Прологарифмируем функцию: ![]() . Берём производную, как производную неявной функции:
. Берём производную, как производную неявной функции: ![]() . Подставляем сюда Y:
. Подставляем сюда Y:
![]() .
.
Ответ: ![]() .
.
16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить ![]() :
:
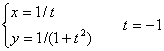 .
.
Уравнения касательной и нормали к кривой ![]() имеют вид
имеют вид ![]() и
и ![]() , где
, где ![]() и
и ![]() - координаты точки касания. Вычислим сначала эти координаты:
- координаты точки касания. Вычислим сначала эти координаты: 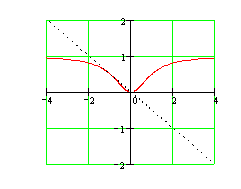
![]() . Найдём производные
. Найдём производные ![]() и
и ![]() :
: ![]()
![]() . Тогда
. Тогда ![]() . Далее,
. Далее, ![]()
![]() , следовательно,
, следовательно, ![]() . Таким образом, уравнение касательной
. Таким образом, уравнение касательной ![]() , уравнение нормали
, уравнение нормали ![]() . Или
. Или ![]() и
и ![]() .
.
Ответ: ![]()
![]()
17. Функция Y(X), заданная неявно уравнением ![]() , принимает в точке
, принимает в точке ![]() значение
значение ![]() . Найти
. Найти ![]() .
.
Дифференцируем уравнение по X, предполагая, что Y= Y(X): ![]() .
.
Из этого равенства находим: ![]() . Находим вторую производную:
. Находим вторую производную:
![]() . Тогда точке
. Тогда точке ![]() :
: ![]() .
.
Ответ: ![]() ,
, ![]() ,
, ![]() .
.
18. Вычислить приближённое значение функции в заданной точке с помощью дифференциала: ![]() .
.
По определению дифференциала ![]() или, в других обозначениях,
или, в других обозначениях, ![]() . Отсюда получаем формулу для приближённых вычислений:
. Отсюда получаем формулу для приближённых вычислений: ![]() . В данном случае
. В данном случае ![]() . Тогда
. Тогда ![]() . Ответ:
. Ответ: ![]()
19. Вычислить предел с помощью правила Лопиталя: 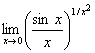 .
.
Неопределённость вида (1∞). Преобразуем предел: 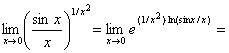
![]() . Найдём предел в показателе степени:
. Найдём предел в показателе степени:
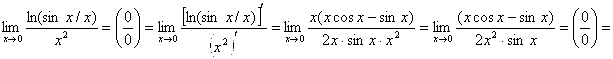
![]() . Следовательно,
. Следовательно, 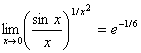 . Ответ:
. Ответ: 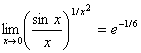 .
.
20. Вычислить предел с помощью правила Лопиталя: ![]() .
.
Это неопределённость вида (∞/∞):
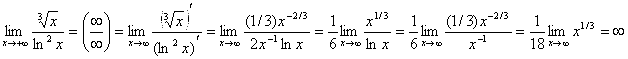 . Ответ:
. Ответ: ![]() .
.
21. Многочлен по степеням X представить в виде многочлена по степеням ![]() :
: ![]() .
.
Запишем формулу Тейлора для многочлена четвёртой степени:
![]() .
.
Найдём все производные: ![]() ,
, ![]() . Тогда
. Тогда ![]() . Подставив это в формулу, получим:
. Подставив это в формулу, получим: ![]() .
.
Ответ: ![]() .
.
22. Найти многочлен, приближающий заданную функцию ![]() в окрестности точки X0 с точностью до
в окрестности точки X0 с точностью до ![]() :
: ![]() .
.
Применяем формулу Тейлора:
![]() .
.
Вычисляем последовательно: ![]()
![]()
![]()
![]() .
.
Ответ: ![]()
23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора: ![]() .
.
Найдём значение функции и её первых четырёх производных в заданной точке:
![]()
![]()
![]() . По формуле Тейлора
. По формуле Тейлора ![]() . Ответ: В окрестности точки (-1, 0) функция ведёт себя как степенная функция четвёртой степени. Точка (-1, 0) является точкой минимума функции.
. Ответ: В окрестности точки (-1, 0) функция ведёт себя как степенная функция четвёртой степени. Точка (-1, 0) является точкой минимума функции.
24. Вычислить предел с помощью формулы Тейлора: ![]() .
.
По формуле Тейлора ![]() . Аналогично,
. Аналогично,
![]() . Подставим это в предел:
. Подставим это в предел: ![]()
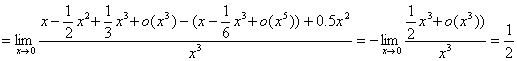 .
.
Ответ: ![]() .
.
 25. Найти асимптоты и построить эскиз графика функции:
25. Найти асимптоты и построить эскиз графика функции: ![]() .
.
Область определения функции: ![]() . Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в граничных точках области определения:
. Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в граничных точках области определения: ![]() . Отсюда следует, что прямые
. Отсюда следует, что прямые ![]() и
и ![]() являются односторонними вертикальными асимптотами. Исследуем функцию при
являются односторонними вертикальными асимптотами. Исследуем функцию при ![]() :
:
![]()
![]() .
.
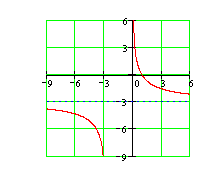
Следовательно, прямая ![]() является горизонтальной асимптотой. Ответ: Эскиз графика представлен на рисунке.
является горизонтальной асимптотой. Ответ: Эскиз графика представлен на рисунке.
26. Провести полное исследование поведения функции и построить её график: ![]() .
.
1. Область определения: ![]() . 2. Функция нечётная, периодичность отсутствует.
. 2. Функция нечётная, периодичность отсутствует. 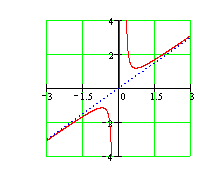 3. Функция непрерывна в области определения. Найдём односторонние пределы в граничных точках области определения:
3. Функция непрерывна в области определения. Найдём односторонние пределы в граничных точках области определения: 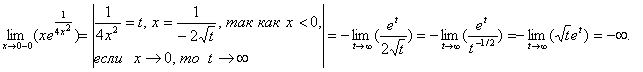 Аналогично,
Аналогично, ![]() Отсюда следует, что прямая
Отсюда следует, что прямая ![]() являются вертикальной асимптотой. 4.
являются вертикальной асимптотой. 4. ![]() . Найдём наклонные асимптоты:
. Найдём наклонные асимптоты: ![]()
![]()
![]() . Следовательно,
. Следовательно, ![]() - наклонная асимптота. 5. Первая производная
- наклонная асимптота. 5. Первая производная ![]() . Производная обращается в нуль в точках
. Производная обращается в нуль в точках ![]() и
и ![]() . При
. При ![]() производная
производная ![]() , следовательно, функция возрастает, при
, следовательно, функция возрастает, при ![]() производная
производная ![]() - функция убывает, при
- функция убывает, при ![]() производная
производная ![]() , следовательно, функция убывает, При
, следовательно, функция убывает, При ![]() производная
производная ![]() , следовательно, функция возрастает. Точка
, следовательно, функция возрастает. Точка ![]() является точкой максимума функции, причём
является точкой максимума функции, причём ![]() . Точка
. Точка ![]() является точкой минимума функции, причём
является точкой минимума функции, причём ![]() .
.
6. 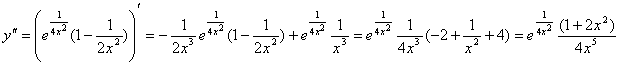 . Вторая производная в нуль не обращается. В точке
. Вторая производная в нуль не обращается. В точке ![]() вторая производная не существует. Имеем два интервала: в интервале
вторая производная не существует. Имеем два интервала: в интервале ![]() производная
производная ![]() - интервал выпуклости, в интервале
- интервал выпуклости, в интервале ![]() производная
производная ![]() - интервал вогнутости. Точек перегиба нет. 7. График функции не пересекает осей координат. Ответ: График функции представлен на рисунке, экстремум в точке
- интервал вогнутости. Точек перегиба нет. 7. График функции не пересекает осей координат. Ответ: График функции представлен на рисунке, экстремум в точке ![]() - максимум, экстремум в точке
- максимум, экстремум в точке ![]() - минимум. Точек перегиба нет.
- минимум. Точек перегиба нет.
| < Предыдущая | Следующая > |
|---|