Вариант контрольной 23

Вариант 23

Задача 1. Вычислить определенный интеграл методом замены переменной с точностью до двух знаков после запятой.

Задача 2. Вычислить определенный интеграл методом интегрирования по частям с точностью до двух знаков после запятой.

Задача 3. Вычислить определенный интеграл с точностью до двух знаков после запятой, выделяя в знаменателе полный квадрат.

Задача 4. Вычислить площадь фигуры, ограниченной графиками функций:

Решение.

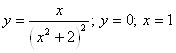
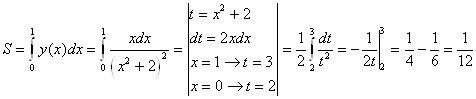
Задача 5. Вычислить площадь фигуры:

Решение.

Фигура (эллипс) симметрична относительно оси 0y, при этом точке , а точке . Поэтому:

Задача 6. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

Решение:

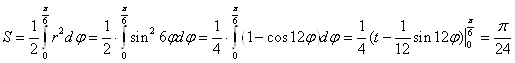
Задача 7.. Вычислить длину дуги кривой:

Решение.

Задача 8. Вычислить длину дуги кривой:

Решение.

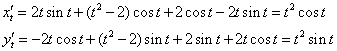
Задача 9. Вычислить длину дуги кривой:

;

Решение.

Задача 10. Вычислить объём тела, ограниченного поверхностями

Решение.

Имеем верхнюю часть двуполостного гиперболоида, т. е. тело с сечениями параллельно XOY, зависящими только от Z:. По оси OZ тело ограничено

Значит, объем тела:

Сечение, перпендикулярное оси OZ – эллипс:

Площадь эллипса:

.

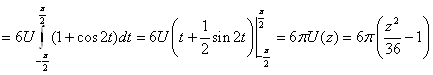Задача 11. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций. Ось вращения OХ.

Решение: Найдем точки пересечения графиков функций

Задача 12. Найти координаты центра масс однородной плоской кривой L: дуга окружности радиусом , стягивающая центральный угол .

Решение: Дуга окружности радиусом в параметрической форме записывается:

Задача 13. Вычислить момент инерции треугольника с основанием и высотой относительно его основания.

Решение: Расположим ось OX по основанию треугольника.

Тогда: , а стороны треугольника запишутся в виде:

Момент инерции треугольника с основанием и высотой относительно его основания, т. е. относительно оси OX:

Задача 14. Вычислить несобственные интегралы или доказать их расходимость:

А)

Подынтегральная функция определена и непрерывна при . Значит, несобственный интеграл:

Несобственный интеграл расходится.

Б)

Подынтегральная функция определена и непрерывна при и При . Значит, несобственный интеграл:

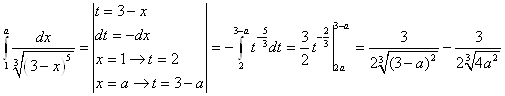
Несобственный интеграл расходится.

Задача 15. Исследовать сходимость интеграла от неотрицательной функции:

Подынтегральная функция определена и непрерывна при .

Оценим подынтегральную функцию при :

Следовательно:

Поскольку интеграл расходится, то по признаку сравнения расходится исходный несобственный интеграл.

< Предыдущая		Следующая >