Вариант № 09

В - 9

Задача 1

А) проверим, является ли линейным подпространством :

Пусть , , и пусть выполняются условия: ;

1) рассм.

И рассм. , след. ;

2) рассм. И рассм. , след. , и след., не является линейным подпространством .

Б) проверим, является ли линейным подпространством :

, , и пусть выполняются условия: ;

1) рассм.

И рассм. , след. ;

2) рассм. И рассм., след. , и след., Является линейным подпространством .

Задача 2

Векторы линейно независимы; проверим, будут ли линейно независимы векторы , где .

Рассм. линейную оболочку (так как линейно независимы) и векторы Служат базисом в ;) рассм. в базисе координаты векторов : ;

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

Ранг матрицы , след. система векторов линейно независима.

Задача 3

;

1) рассм. линейную оболочку ; вычислим ранг системы векторов методом Гаусса:

Рассм. ;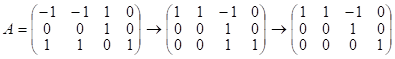

, след. векторы линейно независимы, след. векторы можно считать базисом в ;

2) проверим, принадлежит ли вектор линейной оболочке : вычислим ранг системы векторов :

Рассм. ;

, след. векторы линейно зависимы и .

3) дополним найденный в п. 1) базис до базиса всего пространства : добавим к векторам вектор ; проверим, что ранг системы векторов равен 4 :

Рассм. ;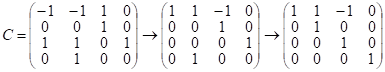

, след. векторы линейно независимы и их можно считать базисом в .

Задача 4

Выписать матрицы и найти .

Пусть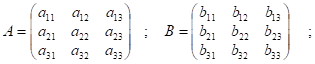

Рассм. усл-е (1):

;

Так как вектор-столбцы совпадают при всех , то получаем:

И матрица имеет вид: ;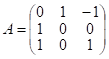

Аналогично, из усл-я (2) получаем:

; ;

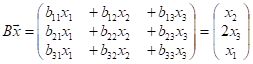Вычислим теперь матрицы:

;

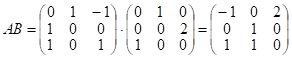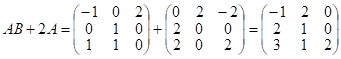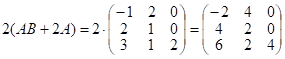
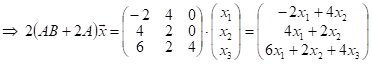Задача 7

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

Имеем ;

Так как , то по теореме Кронекера - Капелли данная система ур-й совместна, а так как , то система имеет бесконечное множество решений;

Объявим свободными переменными и выпишем общее решение системы в коорд. форме:

;

общее решение данной системы ур-й:

Вектор-решение данной системы ур-й: .

Задача 8

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.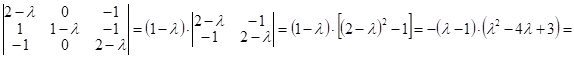

;

- собств. значения (действ.) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм. ;

Рассм.

Положим , тогда вектор ;

Б) рассм.

;

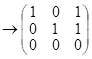Рассм.

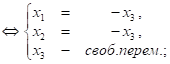
Положим , тогда вектор ;

След., собств. векторы линейного преобразования суть :

; ; .

Задача 9

Привести к каноническому виду кривую 2-го порядка

Уравнение линии 2-го порядка принято записывать в виде:

;

В данной задаче ;

Рассм. ;

Так как , то уравнение (1) – гиперболическое (данная кривая - центральная); выпишем систему уравнений для определения центра кривой :

;

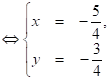
Преобразуем координаты по формулам 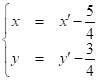(что соответствует переносу начала координат в центр кривой ); уравнение кривой примет вид: ;

;

Выпишем матрицу квадратичной формы и найдём её собственные числа и собственные векторы:

- собств. значения (действ. и различные ) матрицы ;

Найдём собственные векторы матрицы :

Пусть , тогда вектор ;нормируем его и получ. ;

Матрица перехода к базису имеет вид: ;при переходе к базису координаты преобразуются по формулам: ;

Выпишем уравнение кривой в координатах :

;

; ;

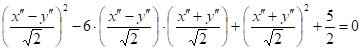- гипербола.

< Предыдущая		Следующая >