Вариант № 05
Задача 1.Найти общее решение дифференциального уравнения.
, (1) – уравнение с разделяющимися переменными
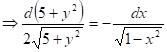
Интегрируя обе части уравнения, получим:
Общее решение уравнения (1): 
Задача 2.Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.
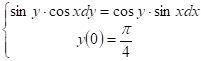
Найдем общее решение дифференциального уравнения с разделяющимися переменными
Интегрируя обе части уравнения, получим:
Общее решение уравнения 
Подставляем в полученное решение начальное условие: 
Значит, искомое частное решение: 
Задача 3. Решить дифференциальное уравнение 
(1) 
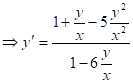
Применим подстановку 
Тогда: 
Интегрируя, получим общий интеграл уравнения 
В результате общий интеграл уравнения имеет вид: 
Подставляя значение , получим общий интеграл уравнения (1): 
Задача 4. Решить дифференциальное уравнение 
(1)
Составим определитель 
Положим 
, где
Определяются из системы уравнений:
Положим в уравнении (1) 
; получим: 
;
Применим подстановку 
; тогда: 
;
Интегрируя обе части уравнения, получим:
Учитывая, что 
, запишем общее решение уравнения (1): 
Задача 5.Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.
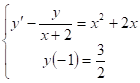
Ищем общее решение линейного неоднородного дифференциального уравнения 1-го порядка
(1)
Найдем общее решение линейного однородного дифференциального уравнения 1-го порядка
Общее решение этого уравнения: 
; Применим метод вариации постоянных: 
;
Дифференцируем Y По X: 
и подставляем полученные значения в уравнение (1):
Следовательно, общее решение линейного неоднородного дифференциального уравнения 1-го порядка: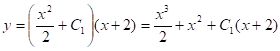 
Подставляем в полученное решение начальное условие: 
Значит, искомое частное решение: 
Задача 6. Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.
Ищем общее решение уравнения Бернулли: 
(1) 
Применим подстановку 
Подставляем в уравнение (1): 
Найдем общее решение линейного однородного дифференциального уравнения 1-го порядка: 
Общее решение этого уравнения: 
; Применим метод вариации постоянных: 
Дифференцируем Y По X: 
Подставляем полученные значения в неоднородное уравнение по Z:
;
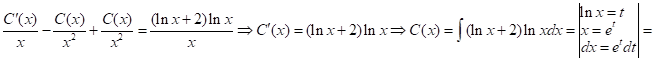
Следовательно, общее решение линейного неоднородного дифференциального уравнения 1-го порядка: 
Следовательно, общее решение уравнения Бернулли (1):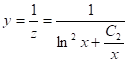 
Подставляем в полученное решение начальное условие: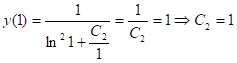 
Значит, искомое частное решение: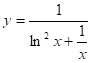 
Задача 7. Найти общий интеграл Дифференциального уравнения.
(1)
То что 
, означает, что мы имеем уравнение в полных дифференциалах
Находим 
Общий интеграл Дифференциального уравнения 
Задача 8. Определить тип дифференциального уравнения, найти общее решение и построить интегральную кривую, проходящую через точку 
.
- Линейное неоднородное дифференциальное уравнение 1-го порядка
Ищем общее решение линейного неоднородного дифференциального уравнения 1-го порядка
(1)
Найдем общее решение линейного однородного дифференциального уравнения 1-го порядка
Общее решение однородного уравнения: 
; Применим метод вариации постоянных: 
;
Следовательно, общим решением является семейство кривых: 
Из условий в точке М найдем: 
Отсюда искомая интегральная кривая: 
Задача 9. Решить дифференциальное уравнение 
(1)
Полагая 
, имеем 
, тогда уравнение (1) принимает вид:
- Линейное неоднородное дифференциальное уравнение 1-го порядка относительно 
.
Найдем общее решение линейного однородного дифференциального уравнения 1-го порядка
Общее решение этого уравнения: 
Задача 10. Найти решение Дифференциального уравнения, удовлетворяющее заданным условиям.
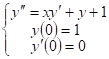
Задача не имеет простого решения, аналогичного другим вариантам, которые решаются методом введения новой переменной. Скорее всего, в условии задачи опечатка.
Задача 11. Найти общее решение дифференциального уравнения 
(1)
- линейное однородное уравнение 2 порядка с постоянными коэффициентами
Характеристическое уравнение: 
Следовательно, фундаментальную систему решений уравнения (1) образуют функции 
общее решение однородного уравнения (1) имеет вид: 
.
Задача 12. Найти частное решение Дифференциального уравнения, удовлетворяющее указанным условиям.
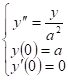
Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами
(1)
Характеристическое уравнение: 
Следовательно, фундаментальную систему решений уравнения (1) образуют функции 
общее решение уравнения (1) имеет вид: 
.
Продифференцируем 
Из указанных условий имеем: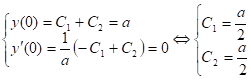 
Частное решение Дифференциального уравнения, удовлетворяющее указанным условиям:
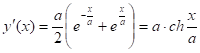
Задача 13. Найти общее решение дифференциального уравнения 
(1)
- линейное неоднородное уравнение 2 порядка с постоянными коэффициентами и специальной правой частью
Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами 
Характеристическое уравнение: 
общее решение однородного уравнения имеет вид: 
.
Структура общего решения неоднородного уравнения (1) имеет вид: 
;
где 
- общее решение однородного уравнения, а функция 
- частное решение неоднородного уравнения.
Так как степень правой части не совпадает с корнем характеристического уравнения, то частное решение ищем в виде: 
Подставляем частное решение в уравнение (1) и находим неопределенные коэффициенты:
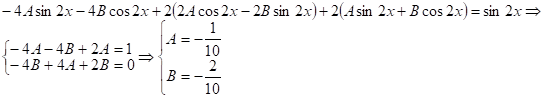
Следовательно, Общее решение неоднородного уравнения (1):
Задача 14. Найти общее решение дифференциального уравнения 
(1)
- линейное неоднородное уравнение 2 порядка с постоянными коэффициентами и специальной правой частью
Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами 
Характеристическое уравнение: 
общее решение однородного уравнения имеет вид: 
.
Применим принцип наложения решений (суперпозиции).
Структура общего решения неоднородного уравнения (1) имеет вид: 
;
где 
- общее решение однородного уравнения, а функции 
- частные решения следующих уравнений:
;
;
Причём частные решения ищем в виде: 
Подставляем поочередно частные решения в соответствующие уравнения и находим неопределенные коэффициенты: 
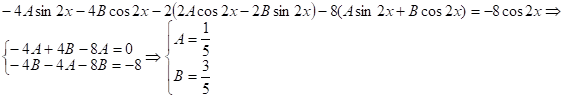
Следовательно, Общее решение неоднородного уравнения (1):
Задача 15. Найти частное решение Дифференциального уравнения, удовлетворяющее указанным условиям.
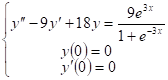
Найдем решение линейного неоднородного уравнения 2 порядка с постоянными коэффициентами 
(1)
Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами
Характеристическое уравнение: 
Следовательно, фундаментальную систему решений однородного уравнения образуют функции 
общее решение однородного уравнения имеет вид: 
.
РЕшение линейного неоднородного уравнения ищем методом вариации произвольных постоянных: 
, а неизвестные функции 
определяем из системы уравнений:
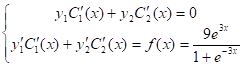
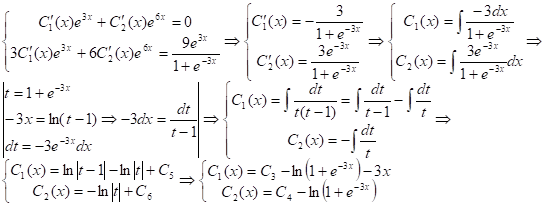
Следовательно, Общее решение неоднородного уравнения (1):
Продифференцируем полученное решение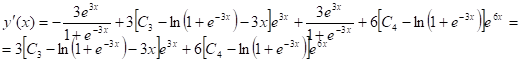 
Из указанных условий имеем: 
Частное решение Дифференциального уравнения, удовлетворяющее указанным условиям:
Задача 16. Найти общее решение дифференциального уравнения 
(1)
- линейное неоднородное уравнение 4-го порядка с постоянными коэффициентами и специальной правой частью (многочлен)
Ищем решение линейного однородного уравнения 4 порядка с постоянными коэффициентами: 
Характеристическое уравнение: 
Следовательно, фундаментальную систему решений уравнения (1) образуют функции 
общее решение однородного уравнения имеет вид: 
.
Частное решение 
Ищем в виде: 
;
Подставляем в неоднородное уравнение (1):
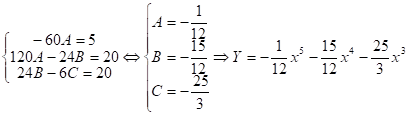
Следовательно, Общее решение неоднородного уравнения (1):
Задача 17. Найти общее решение уравнения Эйлера: 
(1)
Введем новую независимую переменную 
.
Положим 
, тогда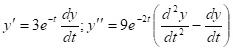 
Подставим в уравнение (1) и получим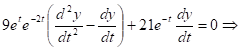 
- линейное однородное уравнение 2 порядка с постоянными коэффициентами.
Характеристическое уравнение: 
общее решение однородного уравнения имеет вид: 
.
Значит, Общее решение уравнения Эйлера (1): 
Задача 18. Решить систему дифференциальных уравнений
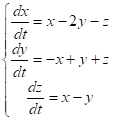(1)
Дифференцируя первое уравнение по , получим: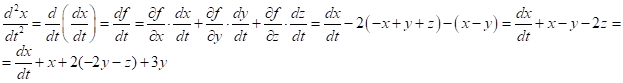 
Из первого уравнения выразим значение 
Значит: 
, а также 
Дифференцируя еще раз уравнение по , получим: 
Из второго уравнения выразим значение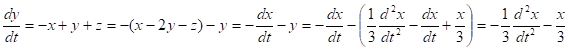 
Подставим полученное значение 
в продифференцированное уравнение:
Получили линейное однородное уравнение 3-го порядка с постоянными коэффициентами 
Характеристическое уравнение: 
Уравнение не имеет целого действительного корня (корень где-то между 0 и -1), поэтому решение нельзя продолжать обычным путем. Скорее всего, в условии задачи опечатка.
| < Предыдущая | Следующая > |
|---|
