Вариант № 16

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Найти угол между диагоналями параллелограмма, построенного на векторах как на сторонах, если

Рассм. рав-во , из к-рого и опр-м ;

Вычислим

;

Задача 3 Вычислить проекцию вектора на ось вектора , Если

Рассм. ;

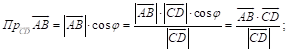
Вычислим ;

Задача 4 Определить, при каком векторы будут взаимно перпендикулярными.

Рассм. .

Задача 5 Найти момент силы, приложенной в точке относительно точки , а также модуль и направляющие косинусы вектора силы

1) , где ;

;

2) ; направл. косинусы вектора :

Задача 6 Найти координаты вектора , если он перпендикулярен векторам , Образует острый угол с осью и .

Пусть , причём ( т. к. Образует острый угол с осью OZ );

;

;

Решим с-му ур-й (1) – (3) и опр-м координаты вектора : но ,

След. выбираем , т. е. и ; .

Задача 7 При каком значении точки будут лежать в одной плоскости?

Рассм. векторы ;

Рассм. смешанное произведение ; след.

При векторы компланарны и точки лежат в одной плоскости.

Задача 8 В треугольнике найти координаты центра тяжести, длину и уравнение медианы , если известны координаты вершин треугольника:

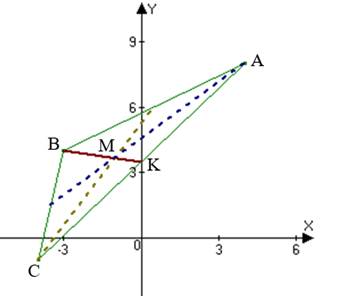
1) Определим координаты точки (середины отрезка ):

; ; ;

2) составим ур – е прямой : ;

3) ;

4) координаты т.Пересечения медиан в (центр масс) определим из условия, что т.Делит отрезок в отношении 2:1, т. е. ; .

Задача 9 Составить уравнения сторон ромба и найти его площадь, если известны уравнения сторон и координаты вершины

1) Составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

2) составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

3) определим площадь ромба :

Определим координаты точки как точки пересечения прямых :

;

Определим координаты точки как точки пересечения прямых :

;

Рассм. векторы: ; рассм. векторное произведение:

Площадь ромба равна: .

Задача 10 Составить уравнение плоскости, проходящей через точки параллельно оси

Пусть - искомая плоскость;

Рассм. вектор ; рассм. направл. вектор оси ;

Рассм. норм. вектор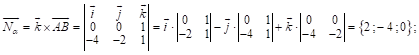

Рассм. произв. т. и рассм. вектор ; , т. е. ; .

Задача 11 Через точку провести прямую , параллельную двум плоскостям: .

Рассм. норм. векторы ;

Рассм. направл. вектор прямой : ;

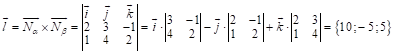Рассм. ; запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. А параллельно вектору : ; параметрические ур-я прямой :

Задача 12 Найти проекцию точки на прямую , заданную как пересечение двух плоскостей:

.

Рассм. норм. векторы ; рассм. направл. вектор прямой :

;

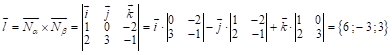Рассм. ; определим какую-либо точку ;

Рассм. Положим , тогда ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. параллельно вектору : ; параметрические ур-я прямой :

Рассм. плоскость , проходящую через точку перпендикулярно прямой : ;

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

Найдём теперь искомую проекцию точки на прямую как точку пересечения плоскости и прямой : ; .

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке:

.

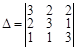1) Непосредственное вычисление:

;

2) Разложение по 1-й строке:

.

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы.

Запишем данную систему уравнений в матричной форме: , (1) , где ; ; ;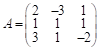

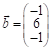Рассм. опред-ль матрицы : ,

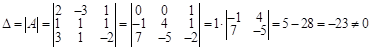След., матр. - невырожденная и можно применять формулы Крамера и вычислять обратную матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул:

, , , где ,

, , ;

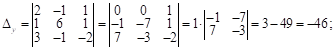
реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. : , след., матр.- невырожденная и существует обратная матр. ; умножим рав-во (1) слева на матрицу :

Вычислим обратн. матр. : находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

;

Транспонируем м-цу и получим «присоединённую» м-цу ;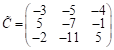

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. ;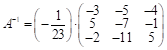

Находим теперь вектор-решение :

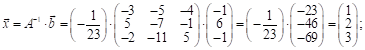
Задача 15 Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

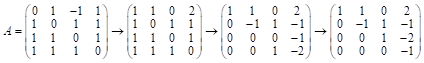; ранг матрицы , след. данная система векторов линейно независима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса:

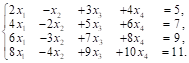
Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

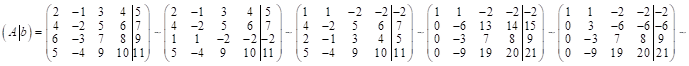
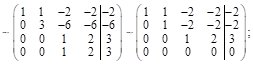имеем ;

Так как , то по теореме Кронекера - Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений;

Объявим Свободной переменной и выпишем общее решение системы в координатной форме:

;

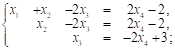
Общее решение системы имеет вид: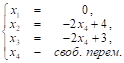

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор - столбцы имеют вид:

Рассм. ;

Вычислим матрицу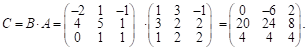

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

- собств. значения (действ. и различные ) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм.

Рассм. 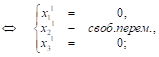Пусть , тогда вектор ;

Б) рассм.

Рассм. Пусть , тогда вектор ;

В) рассм.

Рассм. 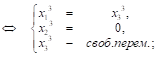Пусть , тогда вектор ;

След. собств. векторы линейного преобразования суть:

; ; .

< Предыдущая		Следующая >