Вариант 14
Вариант 14
1) Разложить функцию, заданную графиком, в ряд Фурье. Построить график суммы полученного ряда Фурье и записать 4 первых ненулевых члена этого ряда.
Функцию, заданную графиком, можно представить в виде: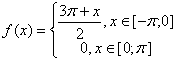 ; Разложим данную функцию в ряд Фурье с периодом
; Разложим данную функцию в ряд Фурье с периодом ![]() :
:
![]()
![]() , где:
, где:

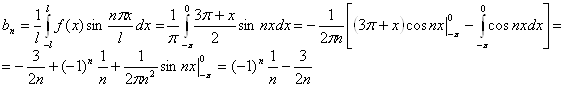
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Сумма ряда ![]() : 1) в точках непрерывности:
: 1) в точках непрерывности: ![]()
2) в точках разрыва: ![]()
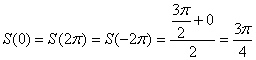
![]()
2) Разложить в ряд Фурье по синусам функцию, определенную на заданном интервале.

Продолжим функцию нечетным образом до периода ![]() :
:
![]()
![]()
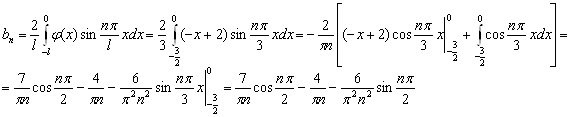
![]() ;
;
![]()
![]()
![]()
![]()
Сумма ряда ![]() : 1) в точках непрерывности:
: 1) в точках непрерывности: ![]()
2) в точках разрыва: ![]() .
.
![]() ;
; 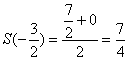 ;
; 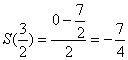
3) Решить задачу Штурма – Лиувилля ![]() . Найти собственные функции, проверить их ортогональность. Разложить функцию
. Найти собственные функции, проверить их ортогональность. Разложить функцию ![]() в ряд по собственным функциям.
в ряд по собственным функциям.
Решение задачи Штурма – Лиувилля ищем в виде: ![]()
Характеристическое уравнение ![]()
1)![]() - кратный корень.
- кратный корень.
Общее решение имеет вид: ![]() ,
, ![]()
Граничные условия: 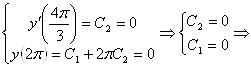
![]()
2) ![]()
![]()
Общее решение имеет вид: ![]()
Граничные условия: 
Т. к. ![]() - тривиальное решение.
- тривиальное решение.
3)![]()
![]()
Общее решение имеет вид: ![]()
Граничные условия: 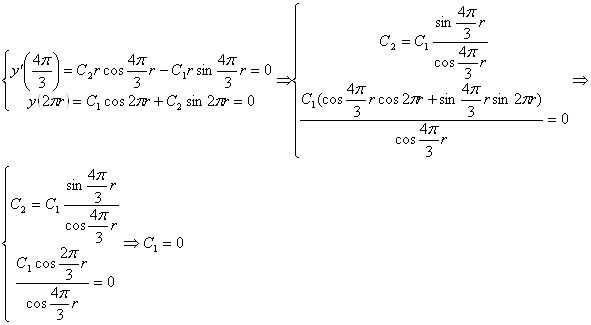
![]()
![]()
Система собственных функций ![]() при
при ![]() ,
,
Где ![]()
Проверка на ортогональность собственных функций

Система собственных функций ![]() ортогональна.
ортогональна.
Разложим ![]() в ряд по собственным функциям
в ряд по собственным функциям ![]() :
:![]()
Согласно теореме Стеклова функцию можно разложить в ряд Фурье: ![]() ,
,
Где 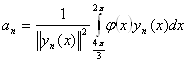
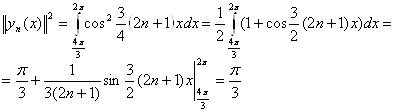
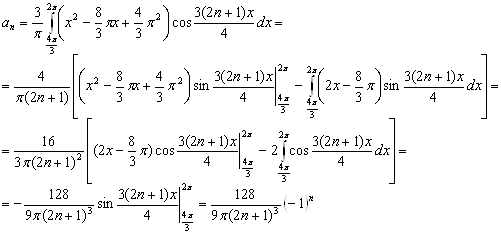
Значит ![]()
4) Решить задачу о свободном колебании струны длины ![]() м с заданными краевыми условиями
м с заданными краевыми условиями ![]() ;
; ![]() . Вычислить приближённое отклонение середины струны при
. Вычислить приближённое отклонение середины струны при ![]() сек, используя для этого первые три ненулевых слагаемых в разложении в ряд функции
сек, используя для этого первые три ненулевых слагаемых в разложении в ряд функции ![]() . Положить
. Положить ![]() .
.
![]() ,
,
Решение
Будем искать решение уравнения свободных колебаний струны ![]() , удовлетворяющее однородным граничным условиям:
, удовлетворяющее однородным граничным условиям: ![]() и начальным условиям
и начальным условиям 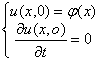 и представимое в виде произведения
и представимое в виде произведения![]() .
.
Подставляем его в исходное уравнение ![]()
Отсюда ![]()
Следовательно: ![]() Граничные условия
Граничные условия 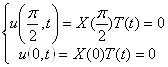
При![]() имеем задачу Штурма – Лиувилля для X(x):
имеем задачу Штурма – Лиувилля для X(x): ![]() .
.
Решение ищем в виде: ![]()
Характеристическое уравнение ![]()
1)![]() - кратный корень.
- кратный корень.
Общее решение имеет вид: ![]()
Граничные условия: 
![]() - тривиальное решение
- тривиальное решение
2) ![]()
![]() , где
, где ![]() - действительное число
- действительное число
Общее решение имеет вид: ![]()
Граничные условия: 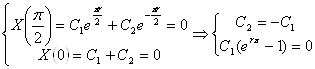
Т. к. ![]() - тривиальное решение.
- тривиальное решение.
3)![]()
![]() ,
, ![]() - действительное число
- действительное число
Общее решение имеет вид: ![]()
Граничные условия: 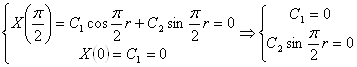
Если ![]()
При этом пусть С2=1, тогда ![]() , при
, при ![]() .
.
Этим же значениям ![]() соответствуют решения уравнения
соответствуют решения уравнения ![]() , имеющие вид:
, имеющие вид:
![]()
Частное решение уравнения свободных колебаний струны:
![]()
Общее решение имеет вид:
![]()
Начальные условия  Значит
Значит ![]()
Разлагаем ![]() в ряд по синусам на промежутке
в ряд по синусам на промежутке ![]() :
: ![]() Сравнивая ряды, видим:
Сравнивая ряды, видим:
 Общее решение представится в виде:
Общее решение представится в виде: ![]()
Приближённое отклонение середины струны ![]() в момент времени to =1:
в момент времени to =1:
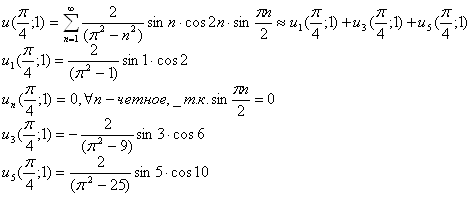
| < Предыдущая | Следующая > |
|---|