Функции двух переменных

Решение

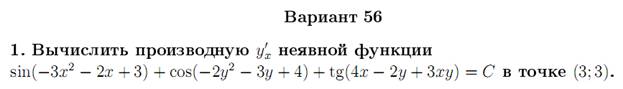
Функция у задана неявно.

Дифференцируем по х равенство

.

Из полученного соотношения

Следует, что

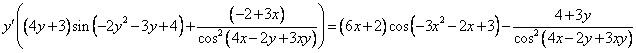
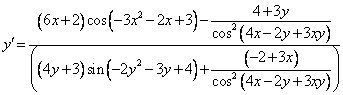или

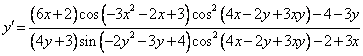
В точке (3;3)

Ответ:

Решение

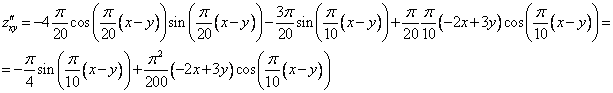
Ответ:

Решение

По формуле

Тогда

, ,

, ,

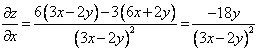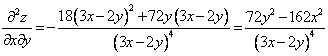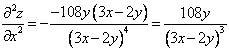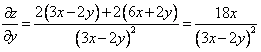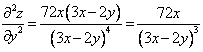
Тогда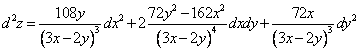

Окончательно

Ответ:

Решение

Если функция  имеет в некоторой окрестности точки непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки из этой окрестности справедлива формула Тейлора n-го порядка: , где

, 

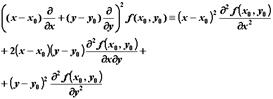
Следовательно, коэффициентом при в окрестности точки будет выражение .

Тогда

Окончательно

Ответ:

Решение

Изобразим данную область

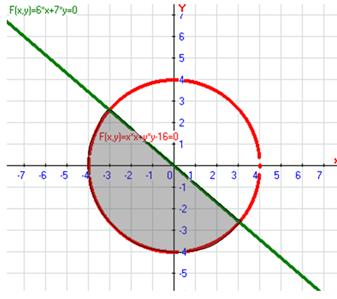
Найдём стационарные точки внутри области

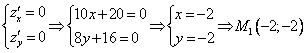
Стационарные точки на границе области

Составим функцию Лагранжа

Для определения точек локального экстремума функции Лагранжа решим систему уравнений

Вычислим значения функции найденных точках

Ответ: Наименьшее значение функции в точке

Решение

Находим частные производные первого порядка

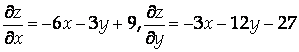
Для нахлждения критических точек решим систему:

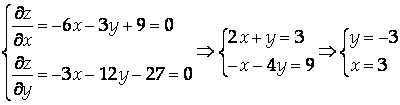
Имеем критическую точку

Найдём экстремальное значение функции:

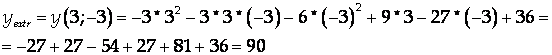
Ответ:

< Предыдущая		Следующая >