Глава 99. Приложение В. Применение MathCad для решения математических задач

Решение системы линейных алгебраических уравнений методом Гаусса:

1. Вводите матрицу системы и матрицу-столбец правых частей.

2. Сформируйте расширенную матрицу системы.

3. Приведите расширенную матрицу системы к ступенчатому виду.

4. Сформируйте столбец решения системы.

Пример

Пусть A - матрица системы, B - матрица-столбец правых частей, Ar - расширенная матрица системы, Ag - расширенная матрица системы в ступенчатом виде, X - столбец решения системы.

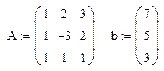
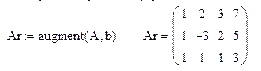
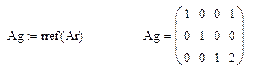
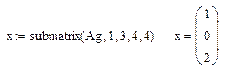
Примечание

ORIGIN := 1 - установка нумерации элементов матриц с единицы.

Augment – функция объединения матриц.

Rref – функция прямого и обратного хода Гаусса.

Submatrix – функция выделения подматрицы с указанными диапазонами из большей матрицы.

Решение системы линейных алгебраических уравнений по формулам Крамера:

1. Вводите матрицу системы и матрицу-столбец правых частей.

2. Вычислите определитель матрицы системы. Если определитель отличен от нуля, то система имеет единственное решение.

3. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.

4. Найдите решение системы по формулам Крамера.

Пример

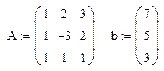
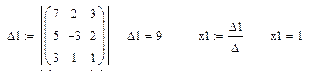
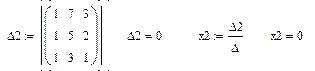
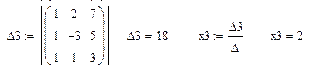
Решение системы линейных алгебраических уравнений матричным методом:

1. Введите матрицу системы и матрицу-столбец правых частей.

2. Определите решение системы по формуле X = A-1B.

Пример

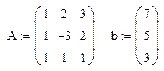
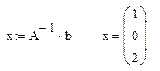
Решение неоднородной системы линейных алгебраических уравнений:

1. Введите матрицу системы и расширенную матрицу системы для правой части.

2. Вычислите ранги основной матрицы и ранги расширенной матрицы системы.

3. Приведите расширенную матрицу совместной системы к ступенчатому виду.

4. Определите базисные и свободные переменные.

5. Запишите эквивалентную систему и разрешите ее относительно базисных переменных.

6. Запишите общее решение системы.

7. Найдите частное решение системы.

Пример

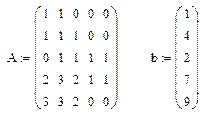
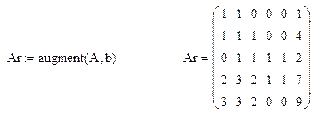
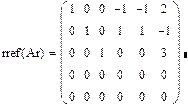
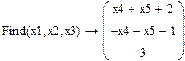
Общее и частное решение системы:

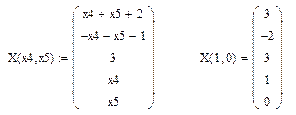
Определение функций

Функция в MathCad должна иметь имя и параметры, перечисленные в скобках. Для получения значения функции в точке, вводится имя функции, указывается в скобках значение аргумента и вводится знак равенства.

Пример

Для ввода составных функций можно пользоваться кнопками панели программирования.

Пример

Построение графиков функций

Для построения графиков функции используется объект X-Y Plot. В помеченной позиции возле оси абсцисс вводится имя аргумента, а в позиции возле оси ординат – имя функции. Если нужно построить одновременно графики нескольких функций, вводятся их имена через запятую. Вместо имени функции можно ввести выражение для ее вычисления. Параметры изображения проще всего изменить, щелкнув дважды по полю графика и установив настройки в соответствующих окнах диалога.

Пример

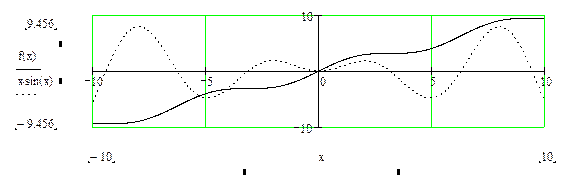
Графики функций, заданных в параметрической форме, строятся аналогично. Отличие состоит в том, что позициях аргумента и функции вводятся выражения или имена соответствующих функций параметра.

Пример

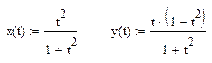
Вычисление пределов

Три нижние кнопки панели Calculus(Вычисление) предназначены для вычисления пределов. Необходимо также пользоваться первой кнопкой со стрелкой на панели символьных операций Symbolic(Символьный).

Пример

Исследование функций

Порядок исследования:

1. Определите функцию f(x) и постройте ее график.

2. Найдите точку пересечения с осью ординат, вычислив f(0). Сравните с данными на графике.

3. Найдите точки пересечения с осью абсцисс, решив уравнение f(x) = 0. Сравните с данными на графике.

4. Проверить четность (нечетность, периодичность) функции.

5. Найдите точки разрыва функции, вычислите соответствующие односторонние пределы, запишите уравнения вертикальных асимптот. Сравните с данными на графике.

6. Вычислите пределы для определения вертикальных и наклонных асимптот. Изобразите наклонные асимптоты на графике.

7. Найдите нули производной, решив уравнение F’(x) = 0.

8. Вычислите и запишите координаты точек экстремума.

9. Постройте график второй производной.

10. Укажите тип точек экстремума (максимум/минимум).

11. Найдите нули второй производной, решив уравнение F’’(x) = 0.

12. Вычислите и запишите координаты точек перегиба.

13. Опишите интервалы выпуклости и вогнутости функции

Пример

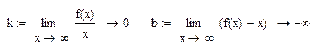
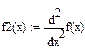
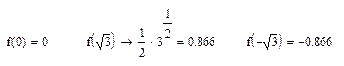
Примечание

Функция root(F(X), X) решает уравнение F(X) = 0 относительно переменной X.

Вычисление интегралов

Для того чтобы вычислить неопределенный или определенный интеграл, необходимо воспользоваться соответствующими кнопками на панели Calculus(Исчисление).

Пример

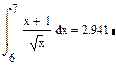
Числовые ряды

Сходимость радов проверяется достаточно легко с помощью кнопки символьных вычислений.

Пример

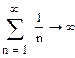
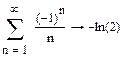
< Предыдущая