Глава 98. Приложение A. Комплексные числа
Рассмотрим двумерное линейное пространство W.
Каждый элемент Z пространства W в некотором базисе однозначно задается двухкомпонентным столбцом ![]() . Если за базисные элементы пространства W принять
. Если за базисные элементы пространства W принять ![]() и
и ![]() , то произвольный элемент
, то произвольный элемент ![]() может быть представлен в виде
может быть представлен в виде ![]() .
.
Введем операцию Умножения элементов пространства W по следующему правилу:
Определение
Результатом операции умножения элементов 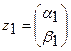 и
и 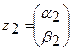 пространства W является элемент также этого пространства
пространства W является элемент также этого пространства 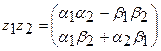 .
.
Определение
Двумерное линейное пространство W, с базисом {![]() ,
, ![]() }, в котором введена операция умножения элементов, называется множеством Комплексных чисел, а каждый элемент
}, в котором введена операция умножения элементов, называется множеством Комплексных чисел, а каждый элемент ![]() W – Комплексным числом.
W – Комплексным числом.
Замечания
1. Операция умножения комплексных чисел коммутативна и обладает распределительным свойством относительно операции сложения, что следует непосредственно из ее определения.
2. Операция умножения комплексных чисел позволяет ввести операцию Деления: частным от деления комплексного числа ![]() на ненулевое
на ненулевое ![]() называется комплексное число
называется комплексное число ![]() такое, что
такое, что ![]() .
.
3. Нетрудно убедиться, что подмножество комплексных чисел вида ![]() , где A – произвольное вещественное число обладает всеми свойствами вещественных чисел, и потому можно говорить, что вещественные числа есть подмножество комплексных чисел.
, где A – произвольное вещественное число обладает всеми свойствами вещественных чисел, и потому можно говорить, что вещественные числа есть подмножество комплексных чисел.
На практике более употребительна специальная, упрощенная форма записи комплексных чисел: в представлении ![]() символ
символ ![]() опускается (как бы заменяется не записываемым явно множителем “Единица”), а символ
опускается (как бы заменяется не записываемым явно множителем “Единица”), а символ ![]() заменяется символом I (называемым иногда “Мнимой единицей”). Тогда произвольное комплексное число Z представимо как
заменяется символом I (называемым иногда “Мнимой единицей”). Тогда произвольное комплексное число Z представимо как ![]() , а записи операций с комплексными числами принимают следующий вид:
, а записи операций с комплексными числами принимают следующий вид:
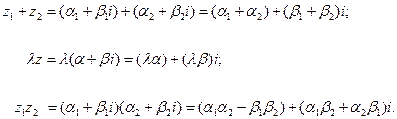
Данная форма записи удобна тем, что с комплексными числами можно оперировать как с обычными алгебраическими двучленами, если принимать во внимание, что ![]() , поскольку
, поскольку
![]() .
.
Тогда, перемножая комплексные числа как двучлены и заменяя повсюду ![]() на число
на число ![]() , мы формально приходим к соотношению
, мы формально приходим к соотношению
![]() ,
,
Которое согласуется с введенным выше определением.
Достаточно просто может выполняться также и операция деления:
![]()
![]() .
.
Определение
Для комплексного числа ![]() :
:
1. Вещественное число A называется Вещественной частью Z и обозначается ![]() .
.
2. Вещественное число B называется Мнимой частью Z и обозначается ![]() .
.
3. Вещественное число ![]() называется Модулем Z и обозначается
называется Модулем Z и обозначается ![]() .
.
4. Вещественное число J такое, что 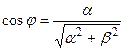 и
и 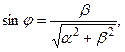 называется Аргументом Z и обозначается
называется Аргументом Z и обозначается ![]() , при условии, что
, при условии, что ![]() .
.
5. Комплексное число ![]() называется Комплексно сопряженным числу z и обозначается
называется Комплексно сопряженным числу z и обозначается ![]() .
.
Замечание 1
Определения, аналогичные пунктам 1, 2 и 5, могут быть сделаны и для матриц, элементами которых являются комплексные числа.
Замечание 2
Поскольку существует взаимно однозначное соответствие множества радиус–векторов на плоскости и множества комплексных чисел, то комплексные числа можно изображать точками на плоскости.
Свойства комплексного сопряжения
1. Имеют место следующие, легко проверяемые свойства для любых ![]() :
:
2. ![]() ;
;
3. Число Z будет вещественным тогда и только тогда, когда ![]() ;
;
4. Число ![]() всегда вещественное и неотрицательное;
всегда вещественное и неотрицательное;
5. ![]() ;
;
6. Если 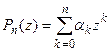 многочлен с вещественными коэффициентами, имеющий корень L, то этот многочлен также будет иметь и корень
многочлен с вещественными коэффициентами, имеющий корень L, то этот многочлен также будет иметь и корень ![]() . Действительно, пусть
. Действительно, пусть ![]() , тогда
, тогда ![]() .
.
Замечание
Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то они попарно сопряжены, а алгебраическое уравнение с вещественными коэффициентами нечетной степени имеет, по крайней мере, один вещественный корень.
Пример
На множестве комплексных чисел решить уравнение ![]() .
.
Перепишем это уравнение, приняв, что ![]() , то есть
, то есть ![]() . Заметим, что здесь мы воспользовались развернутыми представлениями чисел
. Заметим, что здесь мы воспользовались развернутыми представлениями чисел ![]() и
и ![]() .
.
Выполнив умножение и сложение в правой части уравнения, приходим к равенству 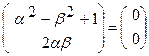 . Но поскольку два комплексных числа равны тогда и только тогда, когда одновременно равны их вещественные и мнимые части, то мы получаем следующую систему нелинейных уравнений относительно вещественных неизвестных A и B :
. Но поскольку два комплексных числа равны тогда и только тогда, когда одновременно равны их вещественные и мнимые части, то мы получаем следующую систему нелинейных уравнений относительно вещественных неизвестных A и B :
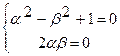 ,
,
Которая, как легко видеть, имеет два решения ![]() и
и ![]() . Поэтому исходное уравнение также имеет два решения
. Поэтому исходное уравнение также имеет два решения ![]() и
и ![]() .
.
Тригонометрическая и экспоненциальная формы записи комплексных чисел
Исходя из определения Пр.3.0.3., можно получить специальную форму записи ненулевых комплексных чисел, называемую Тригонометрической:
![]() .
.
Тригонометрическая форма записи комплексных чисел соответствует заданию точки, изображающей комплексное число, в полярной системе координат.
Пусть
– направляющим элементом полярной оси служит элемент ![]() ,
,
– значение модуля комплексного числа ![]() равно R – расстоянию от начала координат до точки, изображающей данное число,
равно R – расстоянию от начала координат до точки, изображающей данное число,
– значение аргумента ![]() совпадает с величиной полярного угла j, отсчитываемого против часовой стрелки,
совпадает с величиной полярного угла j, отсчитываемого против часовой стрелки,

Рис. A.1
Тогда комплексное число ![]() представимо в тригонометрической форме
представимо в тригонометрической форме
![]() .
.
Другой часто используемой формой представления комплексных чисел, является их Экспоненциальная форма, которая получается преобразованием тригонометрической формы по Формуле Эйлера:
![]() .
.
В этом случае из ![]() следует, что
следует, что ![]() .
.
Использование экспоненциальной формы записи комплексных чисел может упростить решение некоторых задач, поскольку при перемножении комплексных чисел их модули перемножаются, а аргументы складываются).
Например,
![]()
Или
![]() .
.
Пример
Найти какое–либо вещественное решение уравнения ![]() .
.
Решение
Из формулы Эйлера следует, что ![]() , поэтому данное уравнение можно записать в виде
, поэтому данное уравнение можно записать в виде 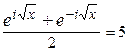 или
или ![]() , где
, где ![]() .
.
Откуда находим, что ![]() , то есть
, то есть ![]() или окончательно
или окончательно ![]() .
.
| < Предыдущая | Следующая > |
|---|