Глава 96. Ряд Маклорена
Теорема
Если функция ![]() может быть разложена на интервале
может быть разложена на интервале ![]() в степенной ряд, то это Разложение единственно.
в степенной ряд, то это Разложение единственно.
Так как по условию теоремы ряд (9.5.3) сходится на интервале ![]() и
и ![]() – его сумма, то в силу свойства 1 этот степенной ряд можно дифференцировать почленно на указанном интервале сколько угодно раз. Тогда, дифференцируя
– его сумма, то в силу свойства 1 этот степенной ряд можно дифференцировать почленно на указанном интервале сколько угодно раз. Тогда, дифференцируя ![]() раз равенство (9.5.3), получаем
раз равенство (9.5.3), получаем
![]() ,
, ![]() ,
,
Откуда при ![]() находим
находим ![]() , или
, или
|
|
(9.5.6) |
Таким образом, коэффициенты степенного ряда (9.5.3) однозначно определяются формулами (9.5.6).
Подстановка полученных коэффициентов в формулу (9.5.3) дает вид разложения функции ![]() в степенной ряд:
в степенной ряд:
|
|
(9.5.7) |
Ряд (9.5.7) называют рядом Маклорена для функции ![]() .
.
Для любой бесконечно дифференцируемой функции можно составить ряд Маклорена.
Установим теперь связь между формулой Маклорена и рядом Маклорена.
Как известно, для любой ![]() раз дифференцируемой функции справедлива формула Маклорена:
раз дифференцируемой функции справедлива формула Маклорена:
![]() ,
,
Где ![]() остаточный член в форме Лагранжа:
остаточный член в форме Лагранжа: ![]() ,
, ![]() ,
, ![]() .
.
Если ![]() частичная сумма ряда Маклорена, то нетрудно видеть, что формула Маклорена может быть представлена в виде
частичная сумма ряда Маклорена, то нетрудно видеть, что формула Маклорена может быть представлена в виде
|
|
(9.5.8) |
Из представления (9.5.8) следует Теорема о сходимости ряда Маклорена.
Теорема
Для того, чтобы для Бесконечно дифференцируемой функции ![]() имело место разложение (9.5.7) в ряд Маклорена на интервале
имело место разложение (9.5.7) в ряд Маклорена на интервале ![]() , необходимо и достаточно, чтобы остаточный член в формуле Маклорена для этой функции стремился к нулю на указанном интервале при
, необходимо и достаточно, чтобы остаточный член в формуле Маклорена для этой функции стремился к нулю на указанном интервале при ![]() :
:
|
|
(9.5.9) |
Разложение элементарных функций в ряд Маклорена
Для того, чтобы разложить функцию в степенной ряд, необходимо найти коэффициенты ряда, определить радиус сходимости ряда и проверить выполнение условия (9.5.9) на интервале ![]() .
.
1. ![]() . При
. При ![]() получаем
получаем ![]() , откуда по формулам (9.5.6)
, откуда по формулам (9.5.6) ![]() . Далее определяем радиус сходимости степенного ряда с найденными коэффициентами.
. Далее определяем радиус сходимости степенного ряда с найденными коэффициентами. ![]() , т. е. степенной ряд сходится на всей числовой прямой.
, т. е. степенной ряд сходится на всей числовой прямой.
2. ![]() .
. ![]() Ряд сходится на всей числовой оси
Ряд сходится на всей числовой оси ![]() .
.
3. ![]() .
. ![]() Ряд сходится на всей числовой оси
Ряд сходится на всей числовой оси ![]() .
.
4. ![]() .
. ![]()
Понятие о функциональной последовательности, функциональный ряд
Определение
Функциональным рядом Называется выражение
|
|
(9.7.1) |
Где ![]() (члены ряда) суть функции одного и того же аргумента X, определенные в некотором промежутке
(члены ряда) суть функции одного и того же аргумента X, определенные в некотором промежутке ![]() .
.
Определение
|
|
(9.7.2) |
Называется Частичной суммой.
Определение
Совокупность значений X, при которых ряд сходится, называется Областью сходимости функционального ряда.
Пример
Найти область сходимости и выражение суммы для ряда
|
|
(9.7.3) |
Запишем частичную сумму ряда (9.7.3) в виде
|
|
(9.7.4) |
Если ![]() , то
, то ![]() при
при ![]() не имеет конечного предела, т. е. ряд (9.7.3) расходится. При
не имеет конечного предела, т. е. ряд (9.7.3) расходится. При ![]() ряд тоже расходится, так как
ряд тоже расходится, так как ![]() попеременно принимает значения 2 и 1.
попеременно принимает значения 2 и 1.
При остальных значениях X (т. е. при ![]() ) ряд (9.7.3) сходится.
) ряд (9.7.3) сходится.
Таким образом область сходимости ряда (9.7.3) есть промежуток ![]() . В этой области сумма S есть функция X, определяемая следующими равенствами:
. В этой области сумма S есть функция X, определяемая следующими равенствами:
|
|
(9.7.5) |
Определение
Если сумма S сходящегося в каждой точке промежутка ![]() ряда (9.7.1) может быть вычислена с некоторой заданной точностью
ряда (9.7.1) может быть вычислена с некоторой заданной точностью ![]() для всех X сразу, начиная с некоторого номера
для всех X сразу, начиная с некоторого номера ![]() , то ряд (9.7.1) сходится на этом промежутке Равномерно.
, то ряд (9.7.1) сходится на этом промежутке Равномерно.
Если же ни один номер N не обеспечивает требуемой точности для всех X сразу, то ряд (9.7.1) сходится на промежутке ![]() Неравномерно.
Неравномерно.
Определение
Функциональный ряд
|
|
(9.7.6) |
Сходящийся в промежутке ![]() , называется Равномерно сходящимся в этом промежутке, если остаток
, называется Равномерно сходящимся в этом промежутке, если остаток ![]() , начиная с некоторого номера N, Одного и того же для всех рассматриваемых значений X, остается по абсолютному значению меньшим любого заранее данного положительного числа E:
, начиная с некоторого номера N, Одного и того же для всех рассматриваемых значений X, остается по абсолютному значению меньшим любого заранее данного положительного числа E:
|
|
(9.7.7) |
(номер N Зависит Только От E).
Если же для некоторого E условию (9.7.7) нельзя удовлетворить (Для всех X сразу) ни при каком значении N, то говорят, что ряд (9.7.6) в промежутке ![]() Сходится неравномерно.
Сходится неравномерно.
Теорема (Признак равномерной сходимости)
Если каждый член ![]() функционального ряда (9.7.1) при любом X, взятом в промежутке
функционального ряда (9.7.1) при любом X, взятом в промежутке ![]() , по абсолютному значению не превосходит положительного числа
, по абсолютному значению не превосходит положительного числа ![]() и если числовой ряд
и если числовой ряд
|
|
(9.7.8) |
Сходится, то функциональный ряд (9.7.1) в этом промежутке Сходится равномерно.
Теорема (непрерывность суммы ряда)
Если все члены ряда
|
|
(9.7.9) |
Равномерно сходящегося в промежутке ![]() , являются Непрерывными функциями, то и Сумма ряда (9.7.9) есть Непрерывная функция в промежутке
, являются Непрерывными функциями, то и Сумма ряда (9.7.9) есть Непрерывная функция в промежутке ![]() .
.
Теорема (интегрирование рядов)
Если сходящийся ряд
|
|
(9.7.10) |
Составленный из функций, непрерывных в промежутке ![]() , Сходится в этом промежутке Равномерно, то его можно Интегрировать почленно. Ряд
, Сходится в этом промежутке Равномерно, то его можно Интегрировать почленно. Ряд
|
|
(9.7.11) |
Равномерно сходится в промежутке ![]() , и сумма его равна интегралу
, и сумма его равна интегралу 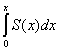 от суммы ряда (9.7.10)
от суммы ряда (9.7.10)
|
|
(9.7.12) |
Теорема (дифференцирование рядов)
Если функциональный ряд
|
|
(9.7.13) |
Сходится в промежутке ![]() и производные его членов непрерывны в этом промежутке, то ряд (9.7.13) можно почленно дифференцировать При условии, что полученный ряд
и производные его членов непрерывны в этом промежутке, то ряд (9.7.13) можно почленно дифференцировать При условии, что полученный ряд
|
|
(9.7.14) |
Будет равномерно сходящимся в данном промежутке. Сумма ряда (9.7.14) будет производной от суммы ряда (9.7.13).
Тригонометрические ряды Фурье
Определение
Тригонометрическим рядом называется ряд вида
|
|
(9.8.1) |
Здесь ![]() – постоянные, называемые Коэффициентами ряда.
– постоянные, называемые Коэффициентами ряда.
Определение
Две функции ![]() называются Ортогональными в промежутке
называются Ортогональными в промежутке ![]() , если интеграл произведения
, если интеграл произведения ![]() , взятый в пределах от A до B, равен нулю.
, взятый в пределах от A до B, равен нулю.
Теорема
Любые две различные функции, взятые из системы функций
|
|
(9.8.2) |
Ортогональны в промежутке ![]() .
.
Пусть дана функции ![]() с периодом
с периодом ![]() . Требуется найти всюду сходящийся тригонометрический ряд
. Требуется найти всюду сходящийся тригонометрический ряд
|
|
(9.8.3) |
Имеющий сумму ![]() .
.
Если эта задача имеет решение, то оно Единственно, и коэффициенты искомого ряда (9.8.3) находятся по формулам Эйлера–Фурье:
|
|
(9.8.4) |
Полученный ряд называется Рядом Фурье для функции ![]() .
.
|
|
(9.8.5) |
Теорема
Если функция ![]() непрерывна на интервале [–L,L], то справедливо разложение
непрерывна на интервале [–L,L], то справедливо разложение
|
|
(9.8.6) |
Где
|
|
(9.8.7) |
Пример
Разложить в ряд Фурье функцию ![]()
Решение
Найдем коэффициенты разложения
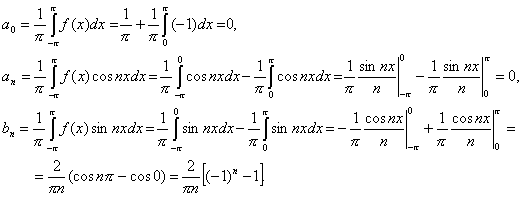
При четных N выражение в квадратной скобке равно нулю, а при нечетных N оно равно –2. Поэтому ![]() . Таким образом
. Таким образом ![]() .
.
96.1. Упражнения
Исследовать сходимость следующих рядов:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
Исследовать сходимость рядов с заданными общими членами
|
5. |
|
6. |
|
Выяснить, какие из нижеследующих рядов сходятся абсолютно:
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
При каких значениях Х Сходятся ряды:
|
11. |
|
12. |
|
| < Предыдущая | Следующая > |
|---|
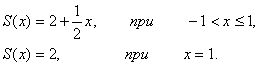
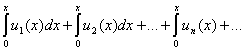
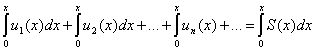
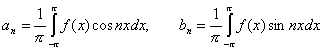
 .
.