Глава 95. Степенные ряды. Область сходимости

В курсе математического анализа изучаются последовательности и ряды, членами которых являются не числа, а функции, определенные на некотором множестве. Такие функциональные последовательности и ряды широко применяются в различных приложениях для анализа и приближенных вычислений. Мы ограничимся рассмотрением степенных рядов.

Определение: Функциональный ряд вида

(9.5.1)

Называется Степенным рядом. Постоянные числа называются Коэффициентами степенного ряда (9.5.1).

При разных значениях переменной мы получим разные числовые ряды, которые могут быть сходящимися или расходящимися. Особый интерес представляет множество значений , при которых ряд (9.5.1) сходится, оно называется Областью сходимости степенного ряда.

Очевидно, что частичная сумма степенного ряда представляет собой Функцию переменной . Стало быть, последовательность частичных сумм является Функциональной последовательностью и сумма ряда (9.5.1) является Функцией переменной : .

Теорема: (Теорема Абеля). Если степенной ряд (9.5.1) Сходится при и , то он Абсолютно сходится при всех , таких, что . Если ряд (9.5.1) Расходится при , то он Расходится И при всех , удовлетворяющих неравенству .

Теорема Абеля примечательна утверждением, что если степенной ряд (9.5.1) сходится при , то он сходится абсолютно всюду на отрезке . Если же – точка расходимости ряда, то он расходится везде вне интервала .

Отсюда следует основополагающая в теории степенных рядов Теорема.

Теорема: Если степенной ряд (9.5.1) Сходится не только при , то существует такое положительное число (возможно, и бесконечное), что ряд Абсолютно сходится в интервале и Расходится везде вне этого интервала.

Число и интервал называются соответственно Радиусом сходимости и интервалом сходимости степенного ряда. Всякий степенной ряд имеет свой радиус сходимости . При вопрос о сходимости должен рассматриваться конкретно для каждого ряда.

Способ определения радиуса сходимости степенного ряда (9.5.1) указывает следующая Теорема.

Теорема

Если для степенного ряда (9.5.1) существует Предел

,

(9.5.2)

То Радиус сходимости этого ряда определяется формулой .

Заметим, что если предел (9.5.2) равен нулю, то степенной ряд сходится на всей числовой прямой, т. е. .

Рассмотрим примеры на Определение радиуса сходимости степенного ряда.

Пример

Определить радиус сходимости ряда .

Решение

Согласно Теореме 3, радиус сходимости этого ряда определяется по формуле , т. е. данный ряд Абсолютно сходится на всей числовой оси.

Пример

Определить радиус сходимости ряда , .

Решение

Радиус сходимости находим . Радиус сходимости данного ряда . Выясним вопрос о сходимости ряда в точке . При подстановке в степенной ряд значения , получим числовой ряд , который имеет различный характер сходимости в зависимости от .

А) при ряд сходится Условно на отрезке как знакопеременный ряд, а на интервале он сходится Абсолютно (т. к. и ряд сходится как сумма геометрической прогрессии со знаменателем ).

Б) При ряд сходится Абсолютно на отрезке .

Пример

Определить радиус сходимости ряда , .

Решение

Получаем: . При получаем, что необходимое условие сходимости числового ряда не соблюдается. Следовательно, данный ряд сходится абсолютно на интервале как сумма геометрической прогрессии со знаменателем меньше единицы.

Пример

Определить радиус сходимости ряда .

Решение

Радиус сходимости ряда: 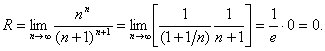Следовательно, данный ряд сходится лишь в точке .

Свойства степенных рядов

Вообще говоря, сумма степенного ряда является функцией от переменной .

.

(9.5.3)

Пусть интервал сходимости этого ряда . Тогда говорят, что функция может быть разложена в степенной ряд на интервале .

Степенные ряды обладают рядом свойств; два из них мы приведем без доказательства.

Степенной ряд можно Дифференцировать почленно на промежутке его сходимости, так что

(9.5.4)

1. При этом интервал сходимости ряда (9.5.4) тот же, что и ряда (9.5.3). Таким же образом можно вычислить производные любого порядка.

2. Степенной ряд можно Интегрировать почленно в интервале его сходимости , т. е. .

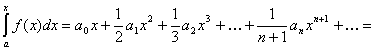
Замечание

Из свойства 1 следует, что сумма степенного ряда непрерывна на интервале его сходимости.

< Предыдущая		Следующая >
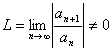