Глава 93. Ряды с положительными членами. Признаки сходимости

Ряды с неотрицательными членами часто встречаются в различных приложениях. Сразу отметим основное свойство таких рядов: Последовательность частичных сумм ряда с неотрицательными членами является неубывающей.

Теорема

Для того чтобы ряд с неотрицательными членами Сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была Ограничена.

Доказательство

По определению сходящегося ряда последовательность его частичных сумм сходится, значит, она необходимо ограничена. Что касается достаточности, то ограниченная монотонная неубывающая последовательность сходится в силу признака сходимости монотонной последовательности.

Определим несколько признаков, позволяющих устанавливать сходимость или расходимость числового ряда.

Теорема

Пусть для двух рядов с неотрицательными членами

	(9.3.1)
	(9.3.2)

Выполняется неравенство для всех . Тогда из Сходимости ряда (9.3.2) следует Сходимость ряда (9.3.1).

Рассмотрим несколько Примеров применения Теоремы 2 по установлению сходимости (расходимости) неотрицательных рядов.

Пример

Исследовать сходимость ряда .

Решение

Поскольку при , а ряд сходится (сумма бесконечно убывающей геометрической прогрессии), то Сходится и данный ряд.

Пример

Исследовать сходимость ряда .

Решение

Так как для достаточно больших (это легко проверить по правилу Лопиталя для функции при , ), то . Ряд расходится, значит Расходится и данный ряд.

Теорема

Пусть ряд (9.3.1) – ряд с неотрицательными членами, а ряд (9.3.2) – ряд с положительными членами. Если существует предел

,

(9.3.3)

То оба ряда Сходятся Или Расходятся одновременно.

Теорема (признак Даламбера)

Пусть для ряда (9.3.1) с положительными членами существует предел

.

(9.3.4)

Тогда этот ряд Сходится при и Расходится при .

Замечание

При необходимо дополнительное исследование ряда с других признаков, так как в этом случае ряд (9.3.1) может как сходится, так и расходится.

В качестве применения признака Даламбера исследуем сходимость следующих рядов.

Пример

Исследовать сходимость ряда , .

Решение

Составим соотношение и перейдем к пределу(9.3.4).

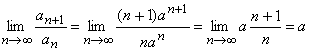. По признаку Даламбера имеем: если . то данный ряд Расходится, если же , то данный ряд Сходится.

Пример

Исследовать сходимость ряда , .

Решение

Находим предел отношения

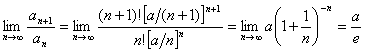
Т. е. при данный ряд Сходится, при он Расходится.

Теорема (признак Коши)

Если существует предел

,

(9.3.5)

То ряд (9.3.1) сходится при и Расходится при .

Пример

Исследовать сходимость ряда 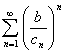, где .

Решение

Применяя признак Коши, получаем 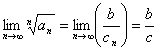. Следовательно, при данный ряд Сходится, а при он Расходится.

Теорема (интегральный признак сходимости)

Пусть функция непрерывная, положительная и убывающая всюду на промежутке . Тогда числовой ряд

(9.3.6)

Сходится вместе с несобственным интегралом

.

(9.3.7)

Пример

Исследовать сходимость ряда , .

Решение

Членами этого ряда являются значения функции в целочисленных точках. Ранее было исследовано, что соответствующий несобственный интеграл первого рода сходится при и расходится при . Следовательно, данный ряд также сходится при и расходится при . В частности, отсюда следует расходимость так называемого Гармонического ряда:

.

< Предыдущая		Следующая >