Глава 68. Условный экстремум. Метод множителей Лагранжа

Пусть рассматривается функция , аргументы X и Y Которой удовлетворяют условию , называемому Уравнением связи.

Определение

Точка называется точкой Условного максимума (Минимума), если существует такая окрестность этой точки, что для всех точек из этой окрестности удовлетворяющих условию , выполняется неравенство .

Точка условного максимума (минимума) не является точкой безусловного экстремума.

Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи удалось разрешить относительно одной из переменных, например, выразить Y Через X: . Подставив полученное выражение в функцию двух переменных, получим , то есть функцию Одной переменной. Ее экстремум и будет условным экстремумом функции .

Пример

Найти точки максимума и минимума функции при условии .

Решение

Выразим из уравнения переменную Y Через переменную X и подставим полученное выражение в функцию Z. Получаем . Эта функция имеет единственный минимум при . Соответствующее значение функции . Таким образом, (3,1) – точка условного экстремума.

В рассмотренном примере уравнение связи оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.

Для отыскания условного экстремума в общем случае используется Метод неопределенных множителей Лагранжа.

Рассмотрим функцию трех переменных .

Эта функция называется Функцией Лагранжа, а l – Множителем Лагранжа.

Теорема

Если точка является точкой Условного экстремума функции при условии , то существует значение l0 такое, что точка является Точкой экстремума функции .

Таким образом, для нахождения условного экстремума функции при условии требуется найти решение системы

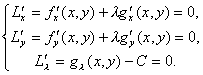
Последнее из этих уравнений совпадает с уравнением связи.

Пример

Найти точки экстремума функции при условии Б используя метод множителей Лагранжа.

Решение

Составляем функцию Лагранжа . Приравняем к нулю ее частные производные, получим систему уравнений

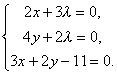
Ее единственное решение . Таким образом, точкой условного экстремума может быть только точка (3,1). Нетрудно убедиться, ч в этой точке функция имеет условный минимум.