Глава 55. Правило Лопиталя
Определение
Будем говорить, что отношение двух функций 
при 
есть Неопределенность вида 
, если 
.
Рис. 5.6.3
Раскрыть эту неопределенность означает Вычислить предел 
, если он существует.
Теорема (Лопиталя)
Пусть функции 
и 
определены и дифференцируемы в некоторой окрестности точки 
, за исключением, быть может, самой точки . Кроме того, пусть также , причем 
в указанной окрестности точки . Тогда если Существует предел отношения 
(конечный или бесконечный), существует и предел , причем справедлива формула:
|
|
(5.7.1) |
=
.Эту теорему обычно называют Правилом Лопиталя.
Замечание 1
Правило Лопиталя можно применить повторно, если 
и 
удовлетворяют тем же требованиям, что и исходные функции и .
Замечание 2
Теорема остается верной и в случае, когда 
).
Пример
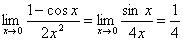
Здесь мы дважды последовательно применили правило Лопиталя, поскольку два раза имели дело с неопределенностью вида .
Неопределенность вида 
Определение
Будем называть отношение двух функций при 
неопределенностью вида , если 
или
. В этом случае правило Лопиталя остается справедливым при замене условия на условие 
.
Пример
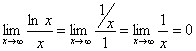
Другие виды неопределенностей
Неопределенности вида 
и 
можно свести к неопределенностям вида и с помощью несложных алгебраических преобразований.
Пример
Найти предел 
.
Здесь имеем неопределенность вида . Преобразуем функцию под знаком предела: 
, в результате имеем неопределенность вида при 
. Теперь, применяя правило Лопиталя, получаем 
.
Неопределенности вида 
, имеющие место при рассмотрении пределов функций 
, сводятся к неопределенностям вида с помощью тождественного преобразования
Пример
Найти предел 
.
Это неопределенность вида 
; используя предыдущую формулу, имеем с учетом только что решенного примера 
.
| < Предыдущая | Следующая > |
|---|
