Глава 54. Основные теоремы дифференциального исчисления – теоремы Ферма, Ролля, Лагранжа

Теорема

Ферма. Пусть функция определена на интервале и имеет наибольшее (наименьшее) значение в точке . Тогда, если в точке существует производная этой функции, то она Равна нулю, т. е. .

Геометрический смысл теоремы Ферма: если в точке дифференцируемая функция принимает наибольшее (наименьшее) значение, то в точке касательная к графику этой функции параллельна оси Ох (Рис. 5.6.1).

Рис. 5.6.1

Заметим, что Теорема неверна, если функция рассматривается на отрезке : в этом случае она может принимать наибольшее и ли наименьшее значение на концах отрезка, где производная не равна нулю.

Теорема (Ролля)

Пусть функция непрерывна на отрезке и дифференцируема на интервале , причем . Тогда существует точка , в которой .

Геометрический смысл теоремы Ролля: если функция, непрерывная на отрезке и дифференцируемая внутри ее, на концах этого отрезка принимает одинаковые значения, то хотя бы в одной внутренней точке этого отрезка касательная к графику функции параллельна оси Ох (Рис. 5.6.2).

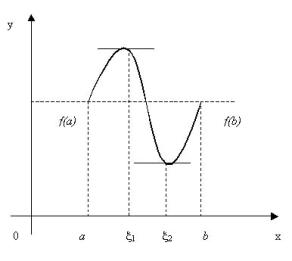
Рис. 5.6.2

Теорема (Лагранжа)

Пусть функция непрерывна на отрезке и дифференцируема на интервале . Тогда существует такая точка , что справедлива формула

.

(5.6.1)

Теорема Лагранжа имеет геометрический смысл (рис. 5.6.3). Секущая, проходящая через точки и , имеет угловой коэффициент, равный , а – угловой коэффициент касательной к графику функции в точке . Теорема Лагранжа утверждает, что существует хотя бы одна точка интервала , где касательная к графику функции параллельна секущей . Приведенные теоремы позволяют сформулировать и обосновать теоремы Лопиталя для раскрытия неопределенностей.

< Предыдущая		Следующая >