Глава 22. Параметрические уравнения прямой

Определение

Всякий вектор, лежащий на прямой, называется Направляющим вектором этой прямой.

Положение прямой на плоскости относительно аффинной системы координат можно определить при помощи некоторой точки прямой и Направляющего вектора , коллинеарного этой прямой (Рис. 2.8.1). Пусть – произвольная точка прямой, тогда

,

(2.8.1)

Где , . Из уравнения (2.8.1) следует, что ,

Рис. 2.8.1

Отсюда находим:

.

(2.8.2)

Таким образом, если прямую задать точкой и направляющим вектором , то координаты любой ее точки находим по формулам (2.8.2).

< Предыдущая		Следующая >
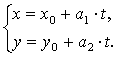