2.1. Основные методы вычисления определенных интегралов

1. Формула Ньютона – Лейбница.

Если - первообразная непрерывной функции на отрезке , то справедлива Формула Ньютона – Лейбница:

. (7)

2.Замена переменной в определенном интеграле.

Пусть требуется вычислить интеграл , где функция непрерывна на отрезке . Полагая , где непрерывно дифференцируемая функция на отрезке , причем , получим:

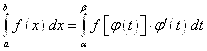. (8)

2. Интегрирование по частям в определенном интеграле.

Если и - непрерывно дифференцируемые функции на отрезке , то справедлива формула интегрирования по частям:

. (9)

Задание 1. Вычислить интеграл: .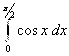

Решение. Так как первообразной подынтегральной функции является функция , то по формуле Ньютона-Лейбница получаем:

.

Задание 2. Вычислить интеграл: .

Решение. Сделаем в данном интеграле замену переменной. Положим , тогда . Найдем новые пределы интегрирования: если , то и, следовательно, ; если , то , и, следовательно, . Тогда имеем:

.

Задание 3. Вычислить интеграл: .

Решение. Воспользуемся формулой интегрирования по частям в определенном интеграле (9). Положим: . Тогда . Следовательно,

.

< Предыдущая		Следующая >