1.7. Интегрирование иррациональных функций

2. Рассмотрим интеграл вида , где-рациональная функция своих аргументов; .

Замена , где , (- наименьшее общее кратное), приводит данный интеграл к интегралу от рациональной функции нового аргумента .

3. Рассмотрим интеграл вида . Для вычисления данного интеграла в квадратичном трехчлене выделяют полный квадрат: . Далее заменой исходный интеграл приводится к одному из следующих интегралов:

, если где

Последние интегралы с помощью соответствующих подстановок:

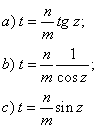
Приводятся к интегралам вида .

Задание 1. Вычислить интеграл: .

Решение. Данный интеграл можно вычислить непосредственным интегрированием. Действительно,

Задание 2. Вычислить интеграл: .

Решение. Данный интеграл не является табличным. Его можно вычислить методом замены переменной. Положим: Тогда , т. е. . Следовательно,

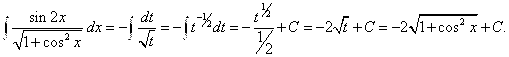
Задание 3. Вычислить интеграл:.

Решение. Данный интеграл не является табличным. Методом замены переменной мы также не достигнем нужного нам результата. Его можно вычислить методом интегрирования по частям. Для этого положим . Тогда . Следовательно, по Формуле интегрирования по частям (2) имеем:

Задание 4. Найти интеграл: .

Решение. Заметим, что подынтегральная функция данного интеграла является правильной рациональной функцией. Разложим её на сумму простейших дробей:

, (3)

Где - неопределенные коэффициенты.

Для нахождения значений коэффициентов правую часть равенства (3) приводим к общему знаменателю:

(4)

Из равенства дробей (3) и (4) получаем:

Два многочлена равны, если равны коэффициенты при одинаковых степенях . Следовательно, имеем:

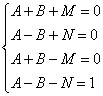(5)

Решив систему алгебраических уравнений (5), получим:

Таким образом, разложение дроби на сумму простейших дробей имеет вид:

Следовательно, исходный интеграл равен:

Задание 5. Найти интеграл: .

Решение. Данный интеграл является интегралом от рациональной функции аргументов и . Полагая , имеем

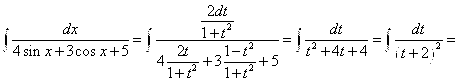
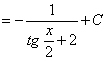Задание 6. Найти интеграл:

Решение. Рассматриваемый интеграл является интегралом от иррациональной функции. Подстановка приведёт данный интеграл к интегралу от рациональной функции аргумента . Действительно имеем: и

Подынтегральная функция полученного интеграла является неправильной рациональной функцией. Чтобы вычислить интеграл, необходимо выделить целую часть дроби и представить эту дробь в виде суммы многочлена и правильной рациональной функции (выполнив деление многочленов). В результате получим:

Следовательно, имеем:

Таким образом,

< Предыдущая		Следующая >