1.6. Интегрирование тригонометрических функций
Интегралы вида 
.
Рассмотрим интеграл вида , где 
-рациональная функция своих аргументов. С помощью подстановки 
данный интеграл сводится к интегралу от рациональной функции переменной 
. Справедливы формулы:
.
Заметим, что подстановка 
является универсальной, так как дает возможность проинтегрировать любую функцию вида . Однако на практике иногда эта подстановка приводит к очень громоздким вычислениям. Поэтому в некоторых частных случаях удобнее использовать другие подстановки:
А) Пусть интеграл имеет вид 
или 
. Тогда соответственно применяется замена 
или 
, которая приводит рассматриваемый интеграл к интегралу от рациональной функции нового аргумента .
Б) Если подынтегральная функция имеет вид , но 
и 
содержатся только в четных степенях, то удобнее воспользоваться подстановкой 
, в результате которой получим интеграл от рациональной функции переменной .
В) Пусть
. Тогда возможны 3 случая:
1) Пусть среди чисел 
и 
есть хотя бы одно нечетное число. Допустим, для определенности, что - нечетное, т. е. 
. Тогда, представив 
и положив , приходим к интегралу, который легко вычисляется.
2) Пусть числа и - четные и неотрицательные. Тогда с помощью формул 
и 
можно понизить степени синуса и косинуса под знаком интеграла: 
;
3) Пусть оба показателя степени и четные, причем хотя бы один из них отрицателен. В этом случае следует сделать замену или 
, в результате которой придем к интегралу, который легко вычисляется.
2. Интегралы вида 
или 
.
Для вычисления данных интегралов используют подстановки или , которые приводят рассматриваемые интегралы к интегралам от рациональных функций нового аргумента .
3. Интегралы вида
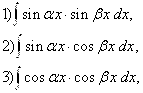
Где
Для вычисления данных интегралов применяются тригонометрические формулы:
| < Предыдущая | Следующая > |
|---|
