20. Лекция 19. Неопределенный интеграл. Основные понятия
Введем операцию, обратную дифференцированию, т. е. по заданной функции ![]() Будем разыскивать функцию
Будем разыскивать функцию ![]() , производная которой равна
, производная которой равна ![]() . Такую функцию будем называть первообразной функцией по отношению к
. Такую функцию будем называть первообразной функцией по отношению к ![]() .
.
Очевидно, что если ![]() ‑ первообразная функции для заданной
‑ первообразная функции для заданной ![]() , то
, то ![]() , где
, где ![]() ‑ некоторая постоянная величина, тоже будет первообразной. Операция нахождения первообразной не является однозначной. Можно легко доказать, что любые две первообразные функции (для одной и той же функции
‑ некоторая постоянная величина, тоже будет первообразной. Операция нахождения первообразной не является однозначной. Можно легко доказать, что любые две первообразные функции (для одной и той же функции ![]() ) отличаются друг от друга на постоянную величину.
) отличаются друг от друга на постоянную величину.
Множество всех первообразных для заданной функции называется Неопределенным интегралом от этой функции и обозначается:
![]() .
.
![]() называется Подынтегральной функцией, а
называется Подынтегральной функцией, а ![]() ‑ Подынтегральным выражением.
‑ Подынтегральным выражением.
Если ![]() ‑ одна из первообразных для
‑ одна из первообразных для ![]() , то можно записать:
, то можно записать:
![]() .
.
Операция нахождения первообразной по-другому называется интегрированием, термин "Неопределенный интеграл" еще раз подчеркивает неоднозначность этой операции.
Из определения неопределенного интеграла сразу следует, что производная и дифференциал от неопределенного интеграла равны соответственно подынтегральной функции и подынтегральному выражению, т. е.
![]() ,
,
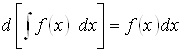 .
.
| < Предыдущая | Следующая > |
|---|