06. Монотонность функции
Функция ![]() называется Возрастающей на промежутке
называется Возрастающей на промежутке ![]() , если
, если ![]() для любых точек
для любых точек ![]() и
и ![]() из промежутка
из промежутка ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() . Функция называется Убывающей на
. Функция называется Убывающей на ![]() , если из условия
, если из условия ![]() следует
следует ![]() .
.
Дифференцируемая функция является возрастающей на промежутке ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Пример 1. Найти промежутки возрастания и убывания функции ![]() .
.
Вычислим ![]() :
: ![]() .
.
Точки 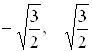 делят числовую прямую
делят числовую прямую ![]() на три интервала:
на три интервала: 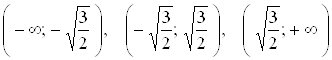 .
.
Производная ![]() положительна на интервалах
положительна на интервалах  . Следовательно, функция
. Следовательно, функция ![]() возрастает на каждом из этих интервалов. На интервале
возрастает на каждом из этих интервалов. На интервале 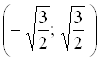 производная
производная ![]() неположительна, значит,
неположительна, значит, ![]() убывает на этом интервале.
убывает на этом интервале.
| < Предыдущая | Следующая > |
|---|