04. Дифференциал
Дифференцируемость функции ![]() в точке
в точке ![]() означает, что ее приращение представлено в виде:
означает, что ее приращение представлено в виде:
![]() .
.
Величина ![]() при малых
при малых ![]() мала по сравнению с величиной
мала по сравнению с величиной ![]() . Поэтому
. Поэтому ![]() представляет собой главную часть приращения
представляет собой главную часть приращения ![]() , называемую Дифференциалом функции в точке
, называемую Дифференциалом функции в точке ![]() . Дифференциал функции
. Дифференциал функции ![]() обозначают обычно символами:
обозначают обычно символами:
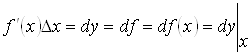 и др.
и др.
Если ![]() ‑ независимая переменная, то
‑ независимая переменная, то ![]() и поэтому
и поэтому ![]() .
.
Вычисление дифференциалов проводят по правилам 1°‑6° дифференцирования с заменой символа ¢ (штрих) на символ ![]() . Например:
. Например:
![]() ;
;
![]() .
.
Пример 7. Вычислить дифференциал функции ![]() в точках
в точках ![]() и
и ![]() .
.
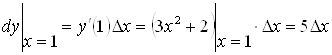 ;
;
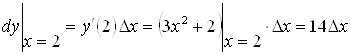 .
.
Таким образом, приращение функции ![]() в точке
в точке ![]() при малых значениях
при малых значениях ![]() приблизительно в пять раз больше, чем
приблизительно в пять раз больше, чем ![]() , а приращение функции в точке
, а приращение функции в точке ![]() приблизительно в 14 раз больше,
приблизительно в 14 раз больше,
чем ![]() .
.
Тот факт, что дифференциал функции является главной частью приращения функции, используют при различны приближенных вычислениях. При этом заменяют приращения функции ![]() ее приближенным значением
ее приближенным значением ![]() . Таким образом,
. Таким образом,
|
|
(2) |
Пример 8. Вычислить ![]() .
.
Рассмотрим функцию ![]() . Заметим, что
. Заметим, что 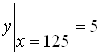 . Возьмем
. Возьмем ![]() . Тогда по формуле (2):
. Тогда по формуле (2):
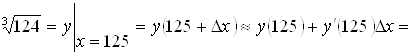
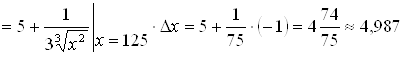 .
.
| < Предыдущая | Следующая > |
|---|