4.1.3 Действия над матрицами
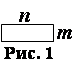 Ранее определили матрицу, как прямоугольную числовую таблицу, имеющую
Ранее определили матрицу, как прямоугольную числовую таблицу, имеющую ![]() строк и
строк и ![]() столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника (рис. 1).
столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника (рис. 1).
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида
 .
.
Две матрицы ![]() и
и ![]() равны, если они одинакового размера и их соответствующие элементы равны.
равны, если они одинакового размера и их соответствующие элементы равны.
Определим основные операции над матрицами.
Определение. Суммой двух матриц ![]() и
и ![]() одинакового размера называется матрица
одинакового размера называется матрица ![]() тех же размеров, элементы которой находятся по формуле
тех же размеров, элементы которой находятся по формуле ![]() . Обозначается
. Обозначается ![]() .
.
Пример 6. 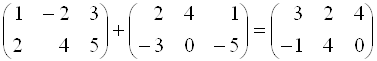 .
.
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что ![]() .
.
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.
Определение. Разностью ![]() матриц
матриц ![]() и
и ![]() одинакового размера называется такая матрица
одинакового размера называется такая матрица ![]() , что
, что ![]() .
.
Определение. Произведением матрицы ![]() на число
на число ![]() называется матрица
называется матрица ![]() , получающаяся из
, получающаяся из ![]() умножением всех ее элементов на
умножением всех ее элементов на ![]() ,
, ![]() .
.
Определение. Пусть даны две матрицы ![]()
![]() и
и ![]() , причем число столбцов
, причем число столбцов ![]() равно числу строк
равно числу строк ![]() . Произведением
. Произведением ![]() на
на ![]() называется матрица
называется матрица ![]() , элементы которой находятся по формуле
, элементы которой находятся по формуле  .
.
Обозначается ![]() .
.
Схематически операцию умножения матриц можно изобразить так:
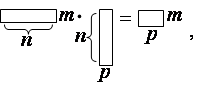
 |
а правило вычисления элемента в произведении:
Подчеркнем еще раз, что произведение ![]() имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго.
имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго.
Пример 7. Даны матрицы 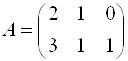 и
и 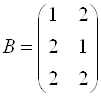 . Найти матрицы
. Найти матрицы ![]() и
и ![]() .
.
Решение. Прежде всего заметим, что произведение ![]() существует, так как число столбцов
существует, так как число столбцов ![]() равно числу строк
равно числу строк ![]() .
.
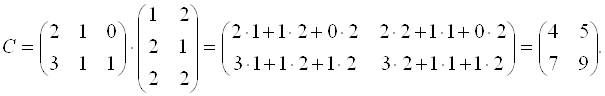
Заметим, что в общем случае ![]() , т. е. произведение матриц антикоммутативно.
, т. е. произведение матриц антикоммутативно.
Найдем ![]() (умножение возможно).
(умножение возможно).

Пример 8. Дана матрица 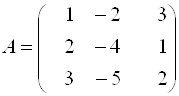 . Найти
. Найти ![]() .
.
 .
.
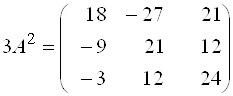 ;
;  .
.
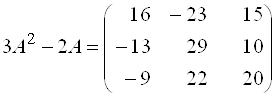 .
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
Пример 9. Если  и
и  , то
, то
 .
.
Определение. Если ![]() – квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая
– квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая ![]() и удовлетворяющая условиям
и удовлетворяющая условиям ![]() , где
, где ![]() – единичная матрица.
– единичная матрица.
Из этого определения следует, что если матрица ![]() является обратной для
является обратной для ![]() , то и
, то и ![]() будет обратной для
будет обратной для ![]() . Обратную матрицу имеет только квадратная матрица, определитель которой отличен от нуля. Такие матрицы называются невырожденными.
. Обратную матрицу имеет только квадратная матрица, определитель которой отличен от нуля. Такие матрицы называются невырожденными.
Приведем схему нахождения обратной матрицы.
1. Находим определитель данной квадратной матрицы ![]() .
.
2. Находим алгебраические дополнения ко всем элементам мат-рицы ![]() .
.
3. Записываем алгебраические дополнения элементов строк в столбцы.
4. Делим каждый элемент полученной матрицы на определитель матрицы ![]() .
.
Пример 10. Найти матрицу, обратную матрице  .
.
Решение.
1. Найдем 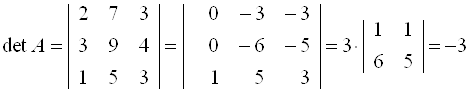 .
.
2. Ищем алгебраические дополнения каждого элемента матрицы ![]() :
:
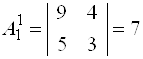 ;
;  ;
; 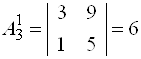 .
.
Получили алгебраические дополнения элементов первой строки. Аналогично для элементов второй и третьей строк получаем:
 ;
;  ;
;  .
.
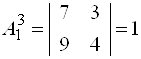 ;
;  ;
;  .
.
Объединяя 3 и 4 пункты, получаем обратную матрицу
 .
.
Для проверки убедимся, что ![]() .
.
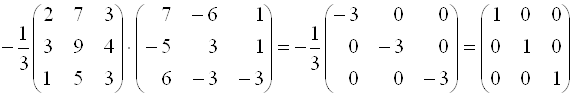 .
.
| < Предыдущая | Следующая > |
|---|