4.1.2 Вычисление определителя - го порядка
Определение. Если в определителе ![]() -го порядка вычеркнуть
-го порядка вычеркнуть ![]() строку и
строку и ![]() столбец, то оставшийся определитель
столбец, то оставшийся определитель ![]() -го порядка называется минором данного элемента
-го порядка называется минором данного элемента ![]() и обозначается
и обозначается ![]() .
.
Определение. Алгебраическим дополнением элемента ![]() определителя
определителя ![]() называется его минор, взятый со знаком
называется его минор, взятый со знаком ![]() .
.
Алгебраическое дополнение элемента ![]() обозначается через
обозначается через ![]() . Следовательно,
. Следовательно, ![]() .
.
Пример 3. Дан определитель  . Найти минор и алгебраическое дополнение элемента
. Найти минор и алгебраическое дополнение элемента ![]() (выделен пунктиром).
(выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент ![]() , получим
, получим  . Тогда
. Тогда ![]() .
.
Теорема 1. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т. е.
![]() , (*)
, (*)
Где ![]() – фиксировано.
– фиксировано.
Выражение (*) называют разложением определителя ![]() по элементам строки с номером
по элементам строки с номером ![]() .
.
Вычисление определителя ![]() -го порядка сводится к вычислению одного определителя
-го порядка сводится к вычислению одного определителя ![]() -го порядка, для чего в какой–либо строке (или столбце) получают
-го порядка, для чего в какой–либо строке (или столбце) получают ![]() нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).
нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).
 |
Пример 4. Вычислить определитель
Наша задача состоит в том, чтобы, пользуясь свойствами определителя, получить максимальное число нулей в какой-нибудь строке или столбце, а затем применить теорему 1. Во второй строке уже имеются два нуля, получим еще нули в этой строке. Для этого прибавим к элементам второго столбца соответствующие элементы четвертого столбца, умноженные на 2, а к элементам третьего столбца прибавим соответствующие элементы четвертого, умноженные на ![]() . Получим определитель, равный исходному
. Получим определитель, равный исходному

 Применим теорему 1 ко второй строке, т. е. разложим определитель по элементам второй строки. Получим определитель 4-го порядка.
Применим теорему 1 ко второй строке, т. е. разложим определитель по элементам второй строки. Получим определитель 4-го порядка.
Теперь получим нули во втором столбце. Для этого к элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на ![]() , а к элементам четвертой – элементы первой, умноженные на
, а к элементам четвертой – элементы первой, умноженные на ![]() .
.
Получим  .
.
Разлагая его по элементам второго столбца, получим
 .
.
Теперь можно разложить полученный определитель, например, по первому столбцу:
 .
.
Легко вычисляются определители квадратных матриц треугольного или диагонального видов. В этом случае определитель равен произведению элементов, расположенных на диагонали.
Квадратная матрица вида  называется диагональной, а квадратные матрицы
называется диагональной, а квадратные матрицы  и
и  называются матрицами треугольного вида.
называются матрицами треугольного вида.
Пример 5. Вычислить определитель

Решение.
Будем получать нули под главной диагональю.
1-й этап. Берем первую строку и с ее помощью получим нули в первом столбце. Первую строку умножим на ![]() и прибавим ко второй, затем первую строку умножим на 2 и прибавим к четвертой. Получим
и прибавим ко второй, затем первую строку умножим на 2 и прибавим к четвертой. Получим

2-й этап. Работаем со второй строкой и получаем нули во втором столбце. Вторую строку умножаем на ![]() и прибавляем к третьей; вторую строку умножаем на 2 и прибавляем к четвертой:
и прибавляем к третьей; вторую строку умножаем на 2 и прибавляем к четвертой:

3-й этап. Из четвертой строки вынесем ![]() и переставим третью и четвертую строки:
и переставим третью и четвертую строки:

И последний этап.
Третью строку умножим на ![]() и прибавим к четвертой:
и прибавим к четвертой:
 .
.
Разлагаем определитель ![]() по элементам первого столбца
по элементам первого столбца
 .
.
Снова разлагаем определитель D по элементам первого столбца:
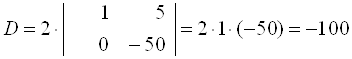 .
.
Действительно, определитель равен произведению элементов, стоящих на диагонали.
Для самостоятельного решения.
1. Вычислить определители
А)  . Ответ:
. Ответ: ![]() .
.
Б)  . Ответ 10.
. Ответ 10.
Указание: Чтобы уменьшить числа, вычтите какую-нибудь строку из остальных. Эту операцию можно проделать несколько раз. Цель: сделать на каком-нибудь месте единицу.
2. Вычислить определитель, приведя его к треугольному виду.
 . Ответ: 52.
. Ответ: 52.
| < Предыдущая | Следующая > |
|---|