1 Определители второго и третьего порядков
Матрицей второго порядка называется таблица
 , (*)
, (*)
Составленная из элементов ![]() .
.
Пары элементов ![]() ,
, ![]() и
и ![]() ,
, ![]() образуют строки матрицы, а пары
образуют строки матрицы, а пары ![]() ,
,![]() и
и ![]() ,
, ![]() – столбцы.
– столбцы.
Матрицей третьего порядка называется таблица, составленная из девяти элементов ![]() :
:  .
.
Матрица, имеющая одинаковое число строк и столбцов, называется квадратной, а число ее строк (столбцов) называется порядком матрицы.
Говорят, что элементы ![]() образуют главную диагональ, а
образуют главную диагональ, а ![]() – побочную.
– побочную.
Число ![]() , составленное из элементов матрицы (*), называют определителем второго порядка и обозначают
, составленное из элементов матрицы (*), называют определителем второго порядка и обозначают  . Таким образом, чтобы сосчитать определитель второго порядка, надо перемножить элементы, стоящие на главной диагонали и вычесть произведение элементов, стоящих на побочной диагонали, например, определитель матрицы
. Таким образом, чтобы сосчитать определитель второго порядка, надо перемножить элементы, стоящие на главной диагонали и вычесть произведение элементов, стоящих на побочной диагонали, например, определитель матрицы  равен
равен  .
.
Определителем третьего порядка  называется число, равное сумме
называется число, равное сумме 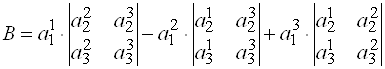 . Это выражение называется разложением определителя по элементам первой строки. Если сосчитать определители второго порядка, то сумма примет вид:
. Это выражение называется разложением определителя по элементам первой строки. Если сосчитать определители второго порядка, то сумма примет вид:
![]()
Можно иначе сосчитать определитель третьего порядка, используя правило Саррюса (правило треугольников).

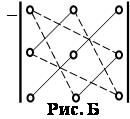 Три слагаемых, входящих в сумму
Три слагаемых, входящих в сумму ![]() со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. А).
со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. А).
Слагаемые, входящие в ![]() со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис. Б).
со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис. Б).
Пример. Вычислить определитель  двумя способами:
двумя способами:
А) разложением по элементам первой строки, б) по правилу Саррюса.
Решение: а) 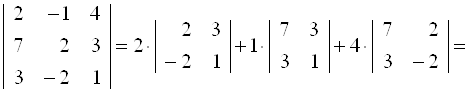
![]()
![]() .
.
Б) 
![]() .
.
Для приобретения навыка, предлагается самостоятельно вычислить следующие определители двумя способами:
1) 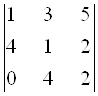 ; Ответ:
; Ответ: ![]() . 2)
. 2) ; Ответ:
; Ответ: ![]() .
.
3)  ; Ответ.
; Ответ. ![]() .
.
| < Предыдущая | Следующая > |
|---|