Экзаменационные задачи по курсу Высшая алгебра. Часть 1
1. Найти матрицу A* оператора сопряженного к линейному оператору A по заданной матрице оператора A и матрице Грамма Г:
А) ![]() :
: ![]() ; б)
; б) 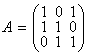 :
: 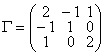 .
.
2. Найти матрицу A* оператора сопряженного к линейному оператору A по заданной матрице оператора A и скалярному произведению:
А) ![]() ,
, ![]() ;
;
Б) ![]() ,
, ![]() ;
;
В) ![]() ,
, ![]() .
.
3. Оператор ![]() переводит векторы A1, A2, в векторы B1, B2, соответственно. Найти оператор A*, если базис в котором заданы
переводит векторы A1, A2, в векторы B1, B2, соответственно. Найти оператор A*, если базис в котором заданы ![]() ,
, ![]() - ортонормирован:
- ортонормирован:
А) ![]() ;
; ![]() ;
;
Б) ![]() ;
; ![]() .
.
4. Оператор ![]() задан матрицей в базисе F1, F2, где F1 = E1 + E2, F2 = E1 – Ie2. Найти A* в том же базисе.
задан матрицей в базисе F1, F2, где F1 = E1 + E2, F2 = E1 – Ie2. Найти A* в том же базисе.
5. Оператор 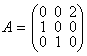 задан матрицей в базисе
задан матрицей в базисе ![]() , где
, где ![]() . Найти
. Найти ![]() в том же базисе.
в том же базисе.
6. В евклидовом пространстве полиномов степени не выше 2 со скалярным произведением ![]() (здесь
(здесь ![]() и
и ![]() коэффициенты полиномов P и Q при
коэффициенты полиномов P и Q при ![]() ) задан оператор
) задан оператор ![]() . Найти
. Найти ![]() в следующих базисах:
в следующих базисах:
а) ![]() ; б)
; б) ![]() .
.
7. В евклидовом пространстве полиномов степени не выше 2 со скалярным произведением 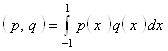 задан оператор
задан оператор ![]() . Найти
. Найти ![]() в следующих базисах: а)
в следующих базисах: а) ![]() ; б)
; б) ![]() .
.
8. Пусть в унитарном пространстве дифференцируемых и периодичных с периодом ![]() функций, скалярное произведение имеет вид:
функций, скалярное произведение имеет вид: 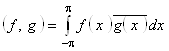 . Доказать, что оператор
. Доказать, что оператор ![]() - эрмитов.
- эрмитов.
9. Установить является ли оператор ![]() самосопряженным, если оператор
самосопряженным, если оператор ![]() задан матрицей в базисе с матрицей Грамма
задан матрицей в базисе с матрицей Грамма ![]() :
:
А) ![]() ; б)
; б) ![]() ;
;
В) ![]() .
.
10. Оператор задан матрицей ![]() в базисе с матрицей Грамма
в базисе с матрицей Грамма ![]() . Будет ли оператор
. Будет ли оператор ![]() - эрмитовым?
- эрмитовым?
11. Установить, является ли ортогональным оператор ![]() , действующий на векторы ортонормированного базиса по формулам:
, действующий на векторы ортонормированного базиса по формулам:
А) ![]() ; б)
; б) ![]() .
.
12. Установить, является ли оператор ![]() унитарным, если
унитарным, если ![]() действует на векторы ортонормированного базиса по формулам:
действует на векторы ортонормированного базиса по формулам:
![]() .
.
13. Установить, является ли ортогональным линейный оператор, заданный в ортонормированном базисе матрицей:
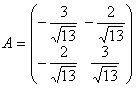 .
.
14. Установить, является ли ортогональным оператор ![]() , если он задан матрицей в базисе
, если он задан матрицей в базисе ![]() , а векторы
, а векторы ![]() выражаются через векторы ортонормированного базиса
выражаются через векторы ортонормированного базиса ![]() :
:
А) ![]() ;
;
Б) ![]() ;
;
В) 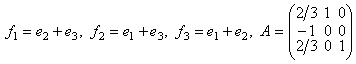 .
.
15. Построить собственный ортонормированный базис самосопряженного оператора, который, в некотором ортонормированном базисе, задан матрицей:
А) ![]() ; б)
; б) ![]() .
.
16. Построить собственный ортонормированный базис эрмитового оператора, который, в некотором ортонормированном базисе, задан матрицей:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
17. Построить собственный ортонормированный базис унитарного оператора, заданного в некотором ортонормированном базисе матрицей:
А) ![]() ; б)
; б) 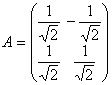 ; в)
; в) 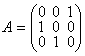 .
.
18. Привести матрицу 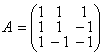 к диагональному виду.
к диагональному виду.
19. Найти:
А) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в) ![]() ,
, ![]() ;
;
Г) ![]() ,
, ![]() ; д)
; д) ![]() ,
, ![]() ; е)
; е) ![]() ,
, ![]() .
.
20. Установить, являются ли следующие квадратичные формы положительно определенными:
А) ![]() ;
;
Б) ![]() .
.
21. Установить, при каких ![]() следующие квадратичные формы являются положительно определенными:
следующие квадратичные формы являются положительно определенными:
А) ![]() ;
;
Б) ![]() .
.
22. Найти ортонормированный базис, в котором следующие квадратичные формы (заданные тоже в ортонормированном базисе) имеют диагональный вид:
А) ![]() ;
;
Б) ![]() .
.
23. Привести следующие квадратичные формы к нормальному виду:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() .
.
24. С помощью одного преобразования привести пару форм к каноническому виду:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() ;
;
Е) ![]() .
.
25. Найти базис, взаимный к данному:
А) ![]() ;
;
Б) ![]() .
.
26. Вектор ![]() задан своими координатами в том же базисе, в котором заданы координаты векторов двух взаимных базисов:
задан своими координатами в том же базисе, в котором заданы координаты векторов двух взаимных базисов: ![]()
![]() и
и ![]() . Найти ковариантные и контравариантные координаты вектора
. Найти ковариантные и контравариантные координаты вектора ![]() .
.
27. Доказать инвариантность свойства антисимметрии тензора второго ранга ![]() .
.
28. Используя тензорную форму записи проверить тождества:
А) ![]() ;
;
Б) ![]() .
.
29. Используя тензорную форму записи, вычислить:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
Д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
(здесь ![]() - постоянные векторы,
- постоянные векторы, ![]() - радиус вектор).
- радиус вектор).
30. Используя тензорную форму записи, доказать тождества:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() .
.
(здесь ![]() - векторные поля,
- векторные поля, ![]() - скалярное поле).
- скалярное поле).
31. Вычислить (используя интегральные теоремы тензорного исчисления) ![]() , где
, где ![]() - постоянные векторы,
- постоянные векторы, ![]() - орт нормали к поверхности
- орт нормали к поверхности ![]() , которая ограничивает объем
, которая ограничивает объем ![]() .
.
32. Найти результат действия перестановок:
А) ![]() ; б)
; б) ![]() ;
;
В) ![]() ; г)
; г) ![]() .
.
32. Возвести перестановки в степень:
а) ![]() ; б)
; б) ![]() ;
;
В) ![]() ; г)
; г) ![]() .
.
33. Найти перестановку, обратную перестановке: ![]() .
.
34. Найти ![]() .
.
35. Найти:
А) ![]() ; б)
; б) ![]()
36. Если ![]() группа перестановок
группа перестановок ![]() чисел, то найти все подгруппы
чисел, то найти все подгруппы ![]() .
.
37. Построить смежные классы к ![]() в
в ![]() , где
, где ![]() и
и ![]() - группы корней 3-й и 6-й степени из 1, соответственно.
- группы корней 3-й и 6-й степени из 1, соответственно.
38. Построить смежные классы к ![]() в
в ![]() , где
, где ![]() и
и ![]() - группы корней 4-й и 8-й степени из 1, соответственно.
- группы корней 4-й и 8-й степени из 1, соответственно.
39. Доказать, что ![]() - нормальный делитель группы
- нормальный делитель группы ![]() , где
, где ![]() и
и ![]() - группы корней 3-й и 6-й степени из 1, соответственно.
- группы корней 3-й и 6-й степени из 1, соответственно.
40. Доказать, что ![]() - нормальный делитель группы
- нормальный делитель группы ![]() , где
, где ![]() и
и ![]() - группы корней 4-й и 8-й степени из 1, соответственно.
- группы корней 4-й и 8-й степени из 1, соответственно.
41. Найти все гомоморфизмы ![]() в
в ![]() , где
, где ![]() группа корней N-й степени из 1.
группа корней N-й степени из 1.
42. Найти фактор-группу ![]() , если:
, если:
а) ![]() - группа целых чисел,
- группа целых чисел, ![]() - подгруппа чисел, кратных заданному целому
- подгруппа чисел, кратных заданному целому
числу ![]() ;
;
б) ![]() - группа всех вещественных чисел по сложению,
- группа всех вещественных чисел по сложению, ![]() - подгруппа целых
- подгруппа целых
чисел;
в) ![]() - группа всех комплексных чисел по сложению,
- группа всех комплексных чисел по сложению, ![]() - группа веществен-
- группа веществен-
ных чисел тоже по сложению;
г) ![]() - группа ненулевых комплексных чисел по умножению,
- группа ненулевых комплексных чисел по умножению, ![]() - группа
- группа
положительных вещественных чисел по умножению;
д) ![]() - группа ненулевых комплексных чисел по умножению,
- группа ненулевых комплексных чисел по умножению, ![]() - подгруппа
- подгруппа
чисел по модулю равных 1.
43. Найти нормальную жорданову форму матрицы:
а) 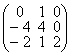 ; б)
; б) 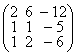 ; в)
; в) 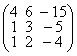 ; г)
; г) 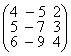 ;
;
д) 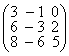 ; е)
; е) 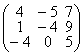 ; ж)
; ж) 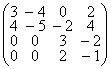 ; з)
; з) 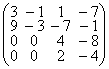 .
.
| < Предыдущая |
|---|