17.18. Тензоры (задачи)

1) Показать, что произведение скаляра на тензор 2-го ранга является тензором 2-го ранга.

2) Показать, что величина (где - тензор 3-го ранга, – тензор 2-го ранга) является вектором.

3) Доказать инвариантность свойств антисимметрии антисимметричного тензора 2-го ранга .

4) Показать, что произведение тензоров 3-го ранга и 2-го ранга является тензором 5-го ранга.

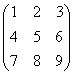5) Компоненты тензора Тik в некотором ортонормированном базисе образуют матрицу и, в том же базисе, вектор В имеет координаты (1,2,3).

А) Разложить тензор ТIk в сумму симметричного SIk и антисимметричного тензоров. б) Найти:

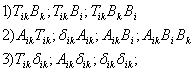
6) Пользуясь аппаратом тензорной алгебры, проверить тождества:

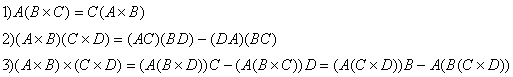
7) Записать в векторной форме выражение:

8) Пользуясь аппаратом тензорной алгебры, проверить тождества:

9) Пользуясь аппаратом тензорной алгебры, вычислить:

(радиус – вектор – , (постоянный вектор – ))

10) Найти дивергенции и роторы следующих векторов:.

(радиус – вектор – , (постоянный вектор – А, B))

11) Вычислить интеграл , где A, C – постоянные вектора, N(R) – орт нормали к поверхности S, которая ограничивает объем V.

< Предыдущая		Следующая >