05.4. Ранг матрицы
Имеется матрица Аmn порядка M´N и не все элементы ее равны 0. ($Aij ¹ 0).
Пусть существует минор RГо порядка, который не равен нулю, и при этом любой минор порядка большего R равен нулю, т. е. $Mr ¹ 0, "Mr + I = 0 (I =1, 2,… , N – R) .
Минор Mr Называется базисным минором матрицы А (он необязательно единственный), строки и столбцы, выбором которых получен минор Называются базисными строками и столбцами, число R Называется рангом матрицы А: R = rangA. Другими словами rangА – это наибольший порядок отличного от нуля минора этой матрицы.
6°. Теорема о базисном миноре. Строки базисного минора – линейно независимы, и любая строка матрицы А является линейной комбинацией базисных строк.
Примечание: Теорема может быть сформулирована и доказана не только для строк, но и для столбцов.
◀ 1) Пусть rangA = R. Не ограничивая общности можно считать, что первые R строк матрицы A1, A2,…, Ar – базисные. Докажем их линейную независимость.
Пусть a1A1 + a2A2 +…+ aRar = q и пусть a1 ¹ 0. Тогда A1 =
, т. е. первая строка является линейной комбинацией остальных, но тогда detMr = 0, что противоречит базисности минора Mr .
Значит a1 = a2 =…= aR = 0 и, следовательно, базисные строки матрицы линейно независимы.
2) Пусть rangA = R и базисный минор Mr стоит в левом верхнем углу:
.
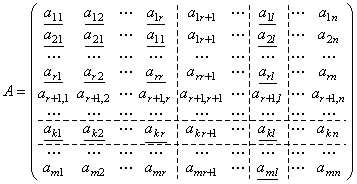Рассмотрим определитель (R + 1)го порядка, состоящий из подчеркнутых элементов: Ar+1.
По условию базисности минора Mr detAr+1 = 0.
Разложим определитель Ar+1 по последнему столбцу. A1LA1L + … + ArlArl + AklAkl = 0; При этом Akl ¹ 0 (это detMr). Тогда 
.
Обозначим 
; 
; Akl – это минор Mr и не зависит ни от K, ни от L. AiL — Не зависит от L (при вычитании выбрасывается). Тогда C1, C2, ... Cr Не зависит от L, а зависит только от K. Имеем Akl = С1A1L + с2A2L +...+ crarl. Последнее равенство показывает, что элементы Kй строки выражены через элементы первых R Строк. ▶
Из этой теоремы следует, что:
7°. detA = 0 тогда и только тогда, когда его строки (столбцы) линейно зависимы.
8°. rangA = dimℒ(A1, A2, … , Am) = dimℒ(S1, S2, … , Sn); a1, A2, … , AM – строки; S1, S2, … , SN – столбцы.
| < Предыдущая | Следующая > |
|---|
