05.1. Системы линейных уравнений. Постановка задачи и терминалогия

Требуется найти X1, X2 … Xn удовлетворяющие следующим соотношениям:

.

Здесь AijÎR (I = 1, 2, … , M; J = 1, 2,… , N) и BiÎR (I =1, 2,… , M) – заданные числа.

Введем обозначения: – Главная матрица системы уравнений;

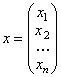– вектор-столбец неизвестных; – вектор-столбец правых частей.

При таких обозначениях система может быть записана в матричной форме: Ax = b.

Вектор 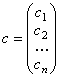Называется решением системы Ax = b, если Ac º B.

Если B1 = B2 = … = Bm= 0, то система уравнений Называется однородной.

.

Если хотя бы одно из значений bi (I = 1, …, m) отлично от нуля система уравнений Называется неоднородной.

Матрица Называется расширенной матрицей Системы уравнений.

Если система линейных уравнений имеет хотя бы одно решение, то она называется совместной. Если система линейных уравнений имеет единственное решение, то она Называется определенной.

Вопросы, на которые нам предстоит ответить по отношению к системе линейных уравнений:

А. Совместна ли система, т. е. имеет ли она хотя бы одно решение?

В. При положительном ответе на предыдущий вопрос определена ли система, т. е. будет ли ее решение единственным?

С. Как находить решение системы?

В случае однородной системы на вопрос А, можно ответить сразу:

Однородная система уравнений всегда совместна. Набор X1 = X2 = … = Xn = 0 является решением системы. Такое решение Называется тривиальным решением. Поэтому для однородной системы линейных уравнений вопрос В звучит следующим образом:

Имеет ли система линейных однородных уравнений другие решения, кроме тривиальных?

< Предыдущая		Следующая >