01.03. Группа

Пусть задано некоторое множество G С элементами, вообще говоря, произвольной природы. Пусть на этом множестве корректным образом задана внутренняя операция, т. е. "Х, УÎG $ ZÎG | Z « X ⊕ Y и эта операция удовлетворяет свойствам:

1) (X ⊕ Y)⊕ Z = X⊕(Y ⊕ Z) – ассоциативность;

2) $qÎG | X ⊕ q = X – существование нейтрального элемента;

3) "XÎG, $YÎG | X ⊕ Y = q – существование противоположного элемента.

Множество G с так введенной операцией Называется группой по этой операции.

Если G – группа по сложению, то нейтральный элемент Называется нулевым, а противоположный – Противоположным.

Если G – группа по умножению, то нейтральный элемент Называется единичным, а противоположный – Обратным.

Если, кроме указанных свойств, операция, определенная в G обладает свойством

X ⊕ Y = Y ⊕ X , то группа Называется коммутативной или абелевой группой.

Примеры

1. Множество вещественных (целых, комплексных, рациональных) чисел является абелевой группой по сложению.

2. Множество вещественных чисел с исключенным нулем является группой по умножению.

3. Рассмотрим множество векторов единичной длины на плоскости, и исходящих из на-

Чала координат. Такой вектор характеризуется углом a, который он образует с положите-

Тельным направлением оси абсцисс.

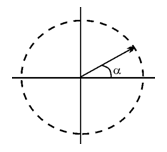
Пусть имеется пара векторов X и Y, характеризующихся углами aХ И aY. Поставим этой паре в соответствие вектор Z, характеризующийся углом aХ+ aY. Указанное множество векторов по операции, введенной выше, образует группу. Эта группа называется группой вращения единичного вектора.

< Предыдущая		Следующая >