7.2. Модифицированный метод Эйлера (метод Рунге-Кутта 2-го порядка)
Для повышения точности формула Эйлера применяется дважды на каждом элементарном отрезке: сначала для вычисления значения функции в середине отрезка ![]() , затем это значение используется для вычисления тангенса угла наклона касательной к графику искомой функции в середине отрезка.
, затем это значение используется для вычисления тангенса угла наклона касательной к графику искомой функции в середине отрезка.
 |
|
|
|
|
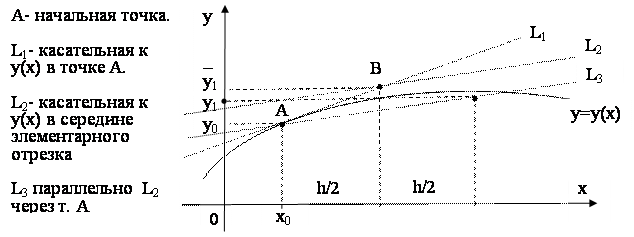
Рис. 7.4. Геометрическая иллюстрация модифицированного метода Эйлера.
Расчётные формулы:
![]() - значение функции в середине отрезка [x0,x1].
- значение функции в середине отрезка [x0,x1].
![]() - значение функции в конце отрезка [x0,x1].
- значение функции в конце отрезка [x0,x1].
Формула модифицированного метода Эйлера:
![]() (7.6)
(7.6)
Где i = 0, 1, …., n-1 - номер узла;
Xi = a + i×h - координата узла;
У0 = у(х0) - начальное условие.
Алгоритм решения ОДУ отличается от описанного ранее алгоритма метода Эйлера (рис 7.3) только алгоритмом расчета новой точки (Рис. 7.5).
Погрешность метода d » О(h3).
Пример 7.2. Решение ранее рассмотренного уравнения (пример 7.1) модифицированным методом Эйлера.
Y’ - 2×y + x2 = 1, x Î [0;1], y(0) = 1.
Пусть n = 10 , h = (1 - 0)/10 = 0,1.
Начальная точка x0 = 0, y0 = 1.
Расчёт первой точки.

Аналогично расчёт следующих точек: 2, 3, ... ,10.
 |
Рис. 7.5. Алгоритм расчёта новой точки модифицированным методом Эйлера:
| < Предыдущая | Следующая > |
|---|